Решебник по геометрии 10 класс Атанасян ФГОС 227

\[\boxed{\mathbf{227.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

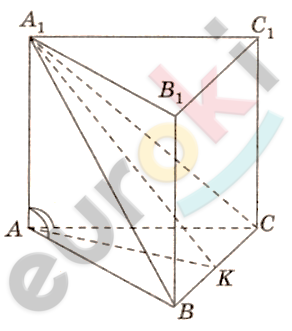
\[Доказать:\]

\[\textbf{а)}\ BC\bot AA_{1};\ \]

\[\textbf{б)}\ CC_{1}B_{1}B - прямоугольник.\]

\[Доказательство.\]

\[\textbf{а)}\ AK - медиана;\ \ AK\bot BC.\]

\[⊿AA_{1}B = ⊿AA_{1}C - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[AA_{1} - общая\ сторона;\]

\[AC = AB;\]

\[\angle A_{1}AC = \angle A_{1}\text{AB.}\]

\[Отсюда:\]

\[A_{1}B = A_{1}C_{1};\]

\[⊿A_{1}BC - равнобедренный.\]

\[A_{1}K - медиана\ и\ высота\ в\ \]

\[равнобедренном\ \]

\[треугольнике:\]

\[A_{1}K\bot BC.\]

\[BC\bot A_{1}K;\ \ BC\bot AK:\]

\[BC\bot\left( A_{1}\text{AK} \right);\]

\[BC\bot A_{1}\text{A.}\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ Четырехугольник\ BB_{1}C_{1}C -\]

\[параллелограмм.\]

\[BC\bot AA_{1};\ \ AA_{1} \parallel BB_{1} \parallel CC_{1}:\]

\[BC\bot B_{1}B;\ \ \ \]

\[BC\bot C_{1}\text{C.}\]

\[Параллелограмм,\ у\ которого\ \]

\[один\ из\ углов\ равен\ 90{^\circ} -\]

\[прямоугольник:\]

\[BB_{1}C_{1}C - прямоугольник.\]

\[Что\ и\ требовалось\ доказать.\]