Решебник по геометрии 10 класс Атанасян ФГОС 228

\[\boxed{\mathbf{228.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

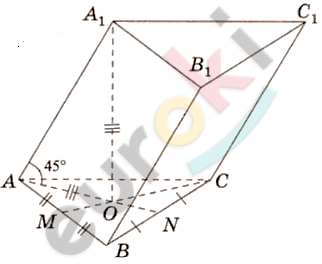
\[Найти:\]

\[S_{BB_{1}C_{1}C}.\]

\[Решение.\]

\[⊿ABC\ (в\ основании) -\]

\[равнобедренный.\]

\[1)\ Из\ вершины\ A_{1}\ проведена\ \]

\[проекция:\]

\[A_{1}O\bot AO.\]

\[⊿A_{1}OA - прямоугольный:\]

\[\angle A_{1}AO = 45{^\circ};\]

\[OA = OA_{1};\]

\[OA = \frac{1}{3}\text{AN.}\]

\[2)\ По\ теореме\ Пифагора\ \]

\[(из\ ⊿ANB):\]

\[AN = \sqrt{AB^{2} - NB^{2}} =\]

\[= \sqrt{169 - 25} = 12\ см;\]

\[OA = 12 \cdot \frac{2}{3} = 8\ см.\]

\[3)\ Из\ треугольника\ A_{1}OA:\]

\[AA_{1} = AO \cdot \sqrt{2} = 8\sqrt{2}\ см.\]

\[4)\ BC\bot\left( A_{1}\text{AO} \right);\ \ BC\bot AA_{1}:\]

\[\text{BC}C_{1}B_{1} - параллелограмм;\]

\[BB_{1} \parallel CC_{1} \parallel AA_{1}.\]

\[Отсюда:\]

\[BC\bot BB_{1};\]

\[BC\bot CC_{1}.\]

\[Значит:\]

\[BB_{1}C_{1}C - прямоугольник.\]

\[5)\ S_{BB_{1}C_{1}C} = BC \cdot BB_{1} =\]

\[= 8\sqrt{2} \cdot 10 = 80\sqrt{2}\ см^{2}.\]

\[Ответ:80\sqrt{2}\ см^{2}.\]