Решебник по геометрии 10 класс Атанасян ФГОС 135

\[\boxed{\mathbf{135.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[a\bot\alpha;\]

\[a\bot b;\]

\[b \notin \text{α.}\]

\[Доказать:\]

\[b \parallel \alpha.\]

\[Доказательство.\]

\[1)\ Через\ точку\ B \in a\ проведем\ \]

\[BK \parallel b.\ \]

\[a\bot b\ и\ BK \parallel b:\]

\[a\bot BK\ (по\ лемме\ п.15).\]

\[2)\ Предположим,\ что\ b \nparallel \alpha,\ \]

\[тогда\ и\ \text{BK\ }не\ параллельна\ a:\]

\[BK \cap \alpha = C.\]

\[3)\ Пусть\ a \cap \alpha = A.\]

\[4)\ Рассмотрим\ \mathrm{\Delta}ABC:\]

\[\angle ABC = 90{^\circ}\ (так\ как\ BC\bot AB);\ \]

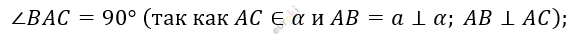
\[Получили,\ что\ в\ \mathrm{\Delta}\text{ABC\ }два\ \]

\[прямых\ угла,\ что\ невозможно.\]

\[Следовательно:\ \]

\[BC \parallel \alpha.\]

\[5)\ BC \parallel b\ и\ BC \parallel \alpha:\ \]

\[b \parallel \alpha.\ \]

\[Что\ требовалось\ доказать.\]