Решебник по геометрии 10 класс Атанасян ФГОС 134

\[\boxed{\mathbf{134.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

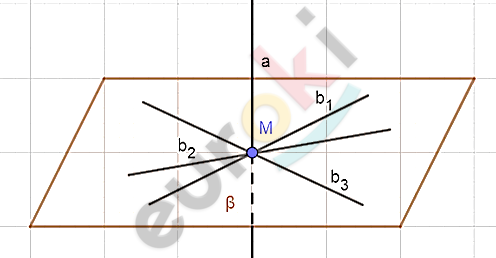
\[Дано:\]

\[M \in a;\]

\[M \in b_{1},b_{2},b_{3};\]

\[b_{1},b_{2},b_{3}\bot a;\]

\[M \in \beta;\]

\[\beta\bot a.\]

\[Доказать:\]

\[b_{1},b_{2},b_{3} \in \text{β.}\]

\[Доказательство.\]

\[1)\ b_{1}\bot a,\ b_{2}\bot a,\ M \in b_{1}\ и\ \]

\[M \in b_{2}:\]

\[b_{1} \cap b_{2} = M.\]

\[По\ признаку\ \]

\[перпендикулярности\ прямой\ и\ \]

\[поскости:\]

\[a\bot\beta.\ \]

\[Через\ 2\ пересекающихся\ \ \]

\[прямых\ можно\ провести\ \]

\[единственную\ плоскость.\]

\[Значит,любая\ прямая\ b_{3},\ \]

\[проходящая\ через\ точку\ \text{M\ }и\]

\[перпендикулярная\ a,\ лежит\ в\ \]

\[плоскости\ \text{β.}\]

\[2)\ Если\ b_{3} \in \beta,\ то\ через\ b_{2}\ и\ b_{3}\ \]

\[можно\ провести\ плоскость\ \alpha:\]

\[a\bot b_{2}\ и\ a\bot b_{3};\]

\[\ a\bot\alpha.\]

\[Тогда\ через\ точку\ M\ проходит\ \]

\[сразу\ две\ плоскости\ \]

\[перпендикулярных\ a,\ но\ через\ \]

\[любую\ точку\ пространства\ \]

\[проходит\ только\ одна\ \]

\[плоскость\ перпендикулярная\ \]

\[данной\ прямой:\]

\[b_{3} \in \beta.\]

\[Что\ и\ требовалось\ доказать.\]