Решебник по геометрии 10 класс Атанасян ФГОС 136

\[\boxed{\mathbf{136.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

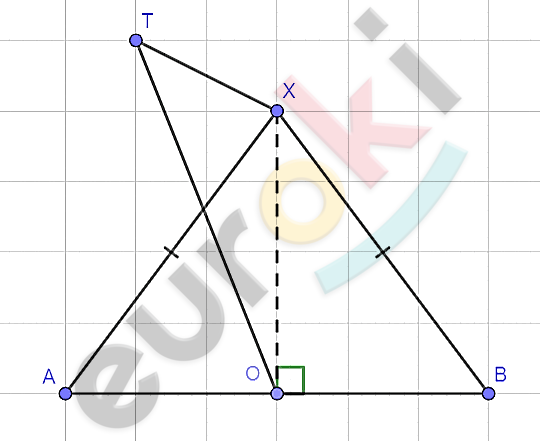
\[Дано:\]

\[X \notin AB;\]

\[AO = OB = \frac{\text{AB}}{2};\]

\[AX = BX.\]

\[Доказать:\]

\[X \in TOX;\]

\[TOX\bot AB.\]

\[Доказательство.\]

\[1)\ \mathrm{\Delta}XAB - равнобедренный:\]

\[AX = BX.\]

\[Опустим\ высоту\ XO:\ \]

\[XO - медиана\ и\ биссектрисса\ \]

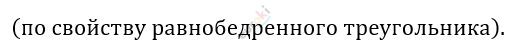
\[Значит:\ \]

\[AO = OB.\]

\[2)\ Построим\ перпендикуляр\ \]

\[TO\bot AXB:\]

\[прямые\ OT\ и\ \text{OX\ }будут\ лежать\ \]

\[в\ одной\ плоскости,\ как\ \]

\[пересекающиеся.\]

\[3)\ AO\bot OX\ и\ \ AO\bot OT:\]

\[AB\bot TOX.\]

\[4)\ AB\bot TOX,\ X \in TOX\ и\ \]

\[O \in TOX:\]

\[ABX\ и\ TOX - пересекаются\ по\ \]

\[прямой\ \text{XO.}\]

\[Что\ и\ требовалось\ доказать.\]