Решебник по алгебре 9 класс Макарычев Задание 776

 

\[\boxed{\text{776\ (776).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ Так\ как\ «в»\ первая\ буква,\ \]

\[то\ остается\ 5\ мест\ для\ \]

\[перестановки:\]

\[P_{5} = 5! = 120\ перестановок.\]

\[\textbf{б)}\ Для\ перестановки\ остается\ \]

\[4\ места:\ \]

\[P_{4} = 4! = 24\ перестановки.\]

\[\boxed{\text{776.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Пусть\ x - числитель\ дроби,\ \]

\[а\ y - знаменатель\ дроби.\ \]

\[При\ этом\ x > 0,\ \ y > 0.\]

\[Составим\ и\ решим\ систему\ \]

\[уравнений:\]

\[\left\{ \begin{matrix} \frac{x - 1}{y - 1} = \frac{x}{y} + \frac{1}{6}\ \\ \frac{x + 1}{y + 1} = \frac{x}{y} - \frac{1}{10} \\ \end{matrix} \right.\ \Longrightarrow\]

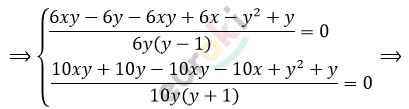
\[\Longrightarrow \left\{ \begin{matrix} - y^{2} - 5y + 6x = 0\ \\ y^{2} + 11y - 10x = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} y^{2} + 5y - 6x = 0 \\ 6y - 4x = 0\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 2x = 3y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ y² + 5y - 9y = 0 \\ \end{matrix} \right.\ \]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{3}{2}\text{y\ \ \ \ \ \ \ \ \ } \\ y² - 4y = 0 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y = 4 \\ x = 6. \\ \end{matrix} \right.\ \]

\[Ответ:дробь = \frac{6}{4}.\]