Решебник по алгебре 9 класс Макарычев Задание 777

 

\[\boxed{\text{777\ (777).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Число\ будет\ четным,\ если\ \]

\[последняя\ цифра - четная:\]

\[то\ есть,6\ или\ 8.\ У\ нас\ \]

\[получается\ два\ варианта,\ \]

\[когда\ на\ первом\ месте\ \]

\[цифры\ стоят\ в\ произвольном\ \]

\[порядке\ (3),\ а\ в\ конце - 6\ или\ 8.\]

\[Если\ на\ конце\ стоит\ цифра\ 6,\ \]

\[то\ получаем:\]

\[P_{3} = 3! = 6\ вариантов.\]

\[Если\ на\ конце\ стоит\ цифра\ 8,\ \]

\[то:\]

\[P_{3} = 3! = 6\ вариантов.\]

\[Найдем,\ сколько\ всего\ \]

\[четырехзначных\ четных\ чисел\ \]

\[можно\ получить:\]

\[6 + 6 = 12\ вариантов.\]

\[Ответ:12\ чисел.\]

\[\boxed{\text{777.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Пусть\ x - это\ числитель\ \]

\[дроби,\ а\ y - ее\ знаменатель.\]

\[Должно\ соблюдаться\ условие,\ \]

\[что\ x > 0,\ y > 0.\]

\[Составим\ и\ решим\ систему\ \]

\[уравнений:\]

\[\left\{ \begin{matrix} \frac{x - 1}{y - 1} = \frac{x}{y} - \frac{1}{10} \\ \frac{x + 1}{y + 1} = \frac{x}{y} + \frac{1}{15} \\ \end{matrix} \right.\ \Longrightarrow\]

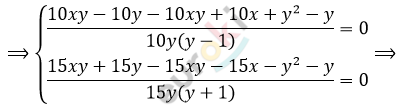
\[\Longrightarrow \left\{ \begin{matrix} y^{2} - 11y + 10x = 0\ \ \\ - y^{2} + 14y - 15x = 0 \\ \end{matrix} \right.\ ( + ) \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 3y - 5x = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ y^{2} - 11y + 10x = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{3}{5}\text{y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ y^{2} - 11y + 6y = 0 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{3}{5}\text{y\ \ \ \ \ \ \ \ \ } \\ y(y - 5) = 0 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} y = 5 \\ x = 3 \\ \end{matrix} \right.\ .\]

\[Наше\ число = \frac{3}{5}.\]

\[Ответ:число\ \frac{3}{5}.\]