Решебник по алгебре 9 класс Макарычев Задание 631

\[\boxed{\text{631.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ c_{5} = c_{1} \cdot q^{4} = - 6,\ \ c_{7} = c_{1} \cdot q^{6} = - 54,\ \]

\[\Longrightarrow \frac{c_{1} \cdot q^{6}}{c_{1} \cdot q^{4}} = \frac{- 54}{- 6};\ \ \ \ q^{2} = 9,\ \ q = \pm 3.\]

\[\textbf{б)}\ c_{6} = c_{1} \cdot q^{5} = 25,\ \ c_{8} = c_{1} \cdot q^{7} = 4,\ \]

\[\frac{c_{8} \cdot q^{7}}{c_{6} \cdot q^{5}} = \frac{4}{25},\ \ q² = \frac{4}{25},\ \ q = \pm \frac{2}{5}.\]

\[\boxed{\text{631.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[Формула\ верна\ при\ n = 1:\ \ \]

\[\frac{1}{n(n + 1)} = \frac{1}{2} = \frac{1}{1 + 1}.\]

\[Допустим,\ что\ при\ n = k,\]

\[\ формула\ тоже\ верна \Longrightarrow\]

\[\Longrightarrow то\ есть,\]

\[\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \ldots + \frac{1}{k(k + 1)} =\]

\[= \frac{k}{k + 1}.\]

\[Докажем,\ что\ формула\ \]

\[справедлива\ для\ n = k + 1:\]

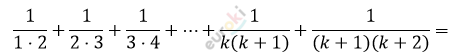
\[= \frac{1}{(k + 1)} + \frac{1}{(k + 1)(k + 2)} =\]

\[= \frac{1}{(k + 1)} \cdot \left( k + \frac{1}{k + 2} \right) =\]

\[= \frac{1}{(k + 1)} \cdot \frac{k^{2} + 2k + 1}{k + 2} =\]

\[= \frac{(k + 1)^{2}}{(k + 1)(k + 2)} =\]

\[= \frac{k + 1}{k + 2} \Longrightarrow ч.т.д.\]