Решебник по алгебре 9 класс Макарычев Задание 628

 

\[\boxed{\text{628\ \ (628).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ 48;12;\ldots\ \]

\[x_{1} = 48;\ \ \ \ \ x_{2} = x_{1} \cdot q = 12\ \ \]

\[48q = 12;\ \ \ \ \ q = \frac{1}{4}\text{\ \ }\]

\[x_{n} = 48 \cdot \left( \frac{1}{4} \right)^{n - 1}\text{\ \ }\]

\[x_{6} = 48 \cdot \left( \frac{1}{4} \right)^{5} = \frac{3}{64}\text{.\ }\]

\[\textbf{б)}\ \frac{64}{9};\ - \frac{32}{3};\ldots\]

\[x_{1} = \frac{64}{9};\ \ \ \ x_{2} = x_{1} \cdot q = - \frac{32}{3}\text{\ \ }\]

\[\frac{64}{9}q = - \frac{32}{3};\ \ \ \ \ \ q = - \frac{3}{2}\]

\[x_{n} = x_{1} \cdot q^{n - 1} = \frac{64}{9} \cdot \left( - \frac{3}{2} \right)^{n - 1}\]

\[x_{6} = \frac{64}{9} \cdot \left( - \frac{3}{2} \right)^{5} = \frac{2^{6}}{3²} \cdot \frac{3^{5}}{2^{5}} = - 2 \cdot 3^{3} = - 54.\]

\[\textbf{в)} - 0,001;\ - 0,01;\ldots\ \]

\[x_{1} = - 0,001;\ \ \ \ x_{2} = x_{1} \cdot q = - 0,01;\ \ \ \ \]

\[- 0,001q = - 0,01;\ \ \ q = 10\]

\[x_{n} = - 0,001 \cdot 10^{n - 1}\]

\[x_{6} = - 0,001 \cdot 10^{5} = - 100.\]

\[\textbf{г)} - 100;10;\ldots.\]

\[x_{1} = - 100;\ \ \ \ \ \ x_{2} = x_{1} \cdot q = 10\ \ \]

\[- 100q = 10;\ \ \ \ \ q = - 0,1\]

\[x_{n} = - 100 \cdot ( - 0,1)^{n - 1}\]

\[x_{6} = x_{1} \cdot q^{5} = - 100 \cdot \left( - \frac{1}{10} \right)^{5} = 10^{2} \cdot 10^{- 5} = 10^{- 3} = 0,001.\]

\[\boxed{\text{628.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\left\{ \begin{matrix} 3x - y \geq 0 \\ y - 5 \geq 0\ \ \\ \end{matrix} \right.\ \]

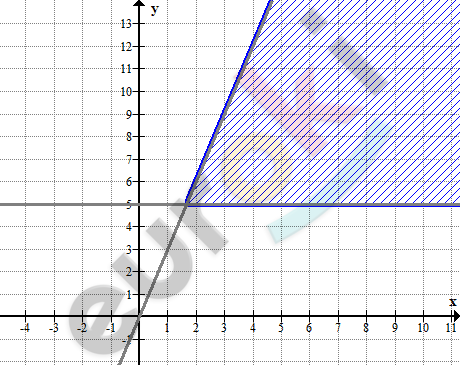
\[Система\ неравенств\ задает\ \]

\[на\ координатной\ прямой\ \]

\[острый\ угол.\]