Решебник по алгебре 9 класс Макарычев Задание 427

 

\[\boxed{\text{427\ (427).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\left( \frac{a + 1^{\backslash a + 1}}{a - 1} - \frac{a - 1^{\backslash a - 1}}{a + 1} \right)\ :\]

\[:\frac{4a}{5a - 5} =\]

\[= \frac{a^{2} + 2a + 1 - a^{2} + 2a - 1}{(a - 1)(a + 1)} \cdot\]

\[\cdot \ \frac{5a - 5}{4a} =\]

\[= \frac{4a}{(a - 1)(a + 1)} \cdot \frac{5 \cdot (a - 1)}{4a} =\]

\[= \frac{5}{a + 1}\]

\[При\ a > - 1:\ \ \]

\[\frac{5}{a + 1} > 0.\ \]

\[Что\ и\ требовалось\ доказать.\]

\(\boxed{\text{427.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\)

\[Схематический\ рисунок\ по\ \]

\[условию\ задачи:\]

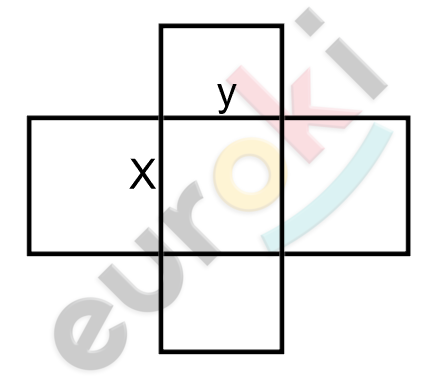
\[Пусть\ длина\ и\ ширина\ \]

\[прямоугольника\ равны\ \]

\[\text{x\ }см\ и\ y\ см.\ Тогда\ \]

\[его\ площадь:\ \ xy = 30.\]

\[Сумма\ площадей\ квадратов:\]

\[2x^{2} + 2y^{2} = 122.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} 2x^{2} + 2y^{2} = 122 \\ xy = 30\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{30}{y}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ x^{2} + y^{2} = 61 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{30}{y}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{900}{y^{2}} + {y^{2}}^{\backslash y^{2}} = 61^{\backslash y^{2}} \\ \end{matrix} \right.\ \]

\[y^{4} - 61y^{2} + 900 = 0\]

\[Пусть\ \ t = y^{2};\ \ t \geq 0:\]

\[t^{2} - 61t + 900 = 0\]

\[D = 61^{2} - 4 \cdot 900 = 121\]

\[t_{1,2} = \frac{61 \pm 11}{2} = 36;25.\]

\[При\ t_{1} = 36:\]

\[y = 6 \Longrightarrow x = 5.\]

\[При\ t_{2} = 25:\]

\[y = 5 \Longrightarrow x = 6.\]

\[Ответ:5\ см\ и\ 6\ см.\]