Решебник по алгебре 9 класс Макарычев Задание 428

 

\[\boxed{\text{428\ (428).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[первого\ велосипедиста,\ \]

\[тогда\ \ (x + 2)\ \frac{км}{ч} -\]

\[скорость\ второго.\ \]

\[\frac{36}{x}\ ч - был\ в\ пути\ первый\ \]

\[велосипедист;\]

\[\frac{36}{x + 2}\ ч - был\ в\ пути\ второй\ \]

\[велосипедист.\]

\[Второй\ велосипедист\ выехал\ \]

\[спустя\ \frac{1}{4}\ часа.\]

\[Составим\ уравнение:\ \]

\[\ \frac{36^{\backslash 4(x + 2)}}{x} - \frac{36^{\backslash 4x}}{x + 2} = \frac{1^{\backslash x(x + 2)}}{4}\]

\[\frac{36 \cdot 4 \cdot (x + 2) - 36 \cdot 4x - x(x + 2)}{4x(x + 2)} = 0\]

\[144x + 288 - 144x -\]

\[- x^{2} - 2x = 0\]

\[- x^{2} - 2x + 288 = 0\]

\[x^{2} + 2x - 288 = 0\]

\[D_{1} = 1 + 288 = 289 = 17^{2}\]

\[x_{1,2} = - 1 \pm 17\]

\[так\ как\ x > 0:\]

\[x = 16\ \left( \frac{км}{ч} \right) - скорость\ \]

\[первого\ велосипедиста.\ \ \]

\[x + 2 = 18\ \left( \frac{км}{ч} \right) - скорость\ \]

\[второго\ велосипедиста.\]

\[Ответ:16\ \frac{км}{ч}\ и\ 18\ \frac{км}{ч}.\]

\(\boxed{\text{428.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\)

\[Схематический\ рисунок\ \]

\[по\ условию\ задачи:\]

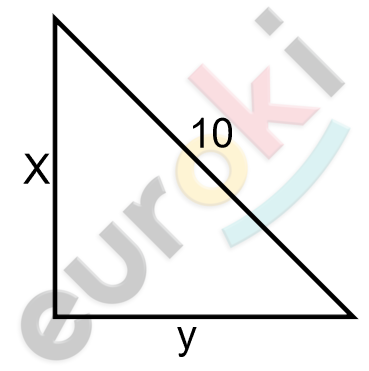
\[Пусть\ катеты\ треугольника\ \]

\[равны\ x\ и\ y\ см.\ \]

\[Тогда\ его\ площадь:\]

\[\frac{1}{2}xy = 24.\ \]

\[По\ теореме\ Пифагора:\]

\[x^{2} + y^{2} = 10^{2}.\]

\[Составим\ систему\ уравнений:\]

\[\left\{ \begin{matrix} xy = 48\ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + y^{2} = 100 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = \frac{48}{y}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{2304}{y^{2}} + y^{2} = 100 \\ \end{matrix} \right.\ \]

\[y^{4} - 100y^{2} + 2304 = 0\]

\[D_{1} = 50^{2} - 2304 = 196\]

\[y_{1,2}^{2} = 50 \pm 14 = 64;36;\]

\[y_{1}^{2} = 64\]

\[y_{1} = 8 \Longrightarrow x_{1} = 6.\]

\[\ y_{2}^{2} = 36\]

\[y_{2} = 6 \Longrightarrow x_{2} = 8.\]

\[Ответ:6\ см\ и\ 8\ см.\]