Решебник по алгебре 9 класс Макарычев Задание 416

 

\[\boxed{\text{416\ (416).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\left\{ \begin{matrix} y - x^{2} = 0\ \ \ \ \ \ \ \ \\ 2x - y + 3 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} y = x^{2}\text{\ \ \ \ \ \ \ } \\ y = 2x + 3 \\ \end{matrix} \right.\ \]

\[Ответ:( - 1;1);\ \ (3;9).\]

\[\boxed{\text{416.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

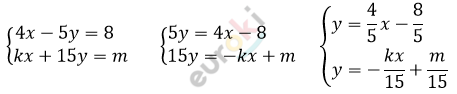
\[\textbf{а)}\ \frac{4}{5}x = - \frac{\text{kx}}{15}\ \ \ \ | \cdot 15\]

\[12x = - kx\]

\[k = - 12.\]

\[\frac{m}{15} \neq - \frac{8}{5}\ \ \ \ \ \ | \cdot 15\]

\[m \neq - 24.\]

\[Ответ:при\ k = - 12;\ \ m \neq - 24.\]

\[\textbf{б)}\ имеет\ бесконечно\ много\ \]

\[решений:\]

\[\frac{4}{5}x = - \frac{\text{kx}}{15}\ \ \ \ | \cdot 15\]

\[12x = - kx\]

\[k = - 12.\]

\[\frac{m}{15} = - \frac{8}{5}\ \ \ | \cdot 15\]

\[m = - 24.\]

\[Ответ:\ при\ k = - 12;\ \ m = - 24.\]

\[\textbf{в)}\ единственное\ решение:\]

\[при\ k \neq - 12;\ \]

\[\ m - любое\ число.\]

\[Ответ:при\ k \neq - 12;\ \ \]

\[m - любое\ число.\]