Решебник по алгебре 9 класс Макарычев Задание 343

 

\[\boxed{\text{343\ (343).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ p^{3} - p^{2} = 8p - 12\]

\[p^{3} - p^{2} - 8p + 12 = 0;\ \ \ \]

\[\ p = 2 \Longrightarrow корень.\]

\[(p - 2)\left( p^{2} + p - 6 \right) = 0\]

\[p^{2} + p - 6 = 0\]

\[D = 1 + 24 = 25\]

\[p_{3,4} = \frac{- 1 \pm 5}{2} = - 3;2.\]

\[Ответ:\ - 3;2.\]

\[\textbf{б)}\ p^{3} - 3p = p^{2} + 1\]

\[p^{3} - p^{2} - 3p - 1 = 0;\ \ \]

\[p = - 1 \Longrightarrow корень.\]

\[(p + 1)\left( p^{2} - 2p - 1 \right) = 0\]

\[p^{2} - 2p - 1 = 0\]

\[D_{1} = 1 + 1 = 2\]

\[p_{2,3} = 1 \pm \sqrt{2}.\]

\[Ответ:\ - 1;1 - \sqrt{2};\ \ 1 + \sqrt{2}.\]

\[\boxed{\text{343.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[(b - 1)x^{2} + 6x + b - 3 = 0\]

\[Квадратное\ уравнение\ не\ \]

\[имеет\ корней,\ если\ D < 0.\]

\[D = 9 - (b - 1)(b - 3) =\]

\[= 9 - \left( b^{2} - 4b + 3 \right) =\]

\[= 9 - b^{2} + 4b - 3 =\]

\[= 6 - b^{2} + 4b\]

\[D < 0:\]

\[b^{2} - 4b - 6 > 0\]

\[D_{1} = 4 + 6 = 10\]

\[b_{1,2} = 2 \pm \sqrt{10}.\]

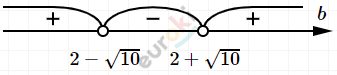
\[b_{1,2} = 2 \pm \sqrt{10} \Longrightarrow\]

\[\Longrightarrow b \in \left( - \infty;2 - \sqrt{10} \right) \cup\]

\[\cup \left( 2 + \sqrt{10}; + \infty \right).\]