Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Макарычев Задание 205
Задание 205
\[\boxed{\text{205\ (205).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[D(y) = \lbrack - 3;4\rbrack;\]
\[E(y) = \lbrack 0;6\rbrack.\]
\[\boxed{\mathbf{205}\text{.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]
\[\textbf{а)}\ y = x² + 2x - 15\]
\[x_{b} = - \frac{b}{2a} = - \frac{2}{2} = - 1;\]
\[y_{b} = ( - 1)^{2} - 2 \cdot 1 - 15 = - 16;\]
\[x^{2} + 2x - 15 = 0\]
\[D = 1 + 15 = 16\]
\[x_{1,2} = - 1 \pm 4\]
\[x_{1} = - 5,\ \ x_{2} = 3\]
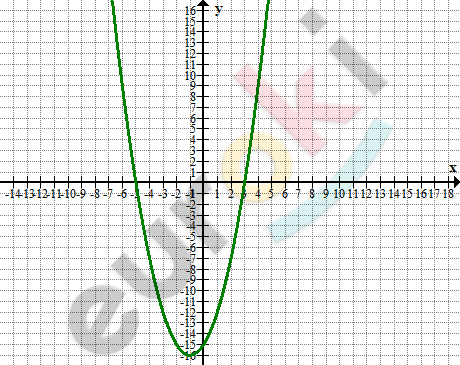
\[E(y) = \ \lbrack - 16;\ + \infty).\]
\[При\ x \in ( - \infty; - 1)\ функция\ \]
\[убывает\ и\ при\ x \in ( - 1; + \infty)\ \]
\[возрастает.\]
\[y < 0\ \ при\ x \in ( - 5;3)\ и\ y > 0\ \ \]
\[при\ \ x \in ( - \infty; - 5) \cup (3; + \infty).\]
\[\textbf{б)}\ y = 0,5x² - 3x + 4\]
\[x_{b} = - \frac{b}{2a} = - \frac{- 3}{- 2 \cdot 0,5} = 3;\]
\[y_{b} = 0,5 \cdot 3^{2} - 3 \cdot 3 + 4 = - 0,5\]
\[0,5x^{2} - 3x + 4 = 0\]
\[D = 9 - 0,5 \cdot 16 = 1\]
\[x_{1,2} = \frac{3 \pm 1}{2 \cdot ,05} = 4;2.\]
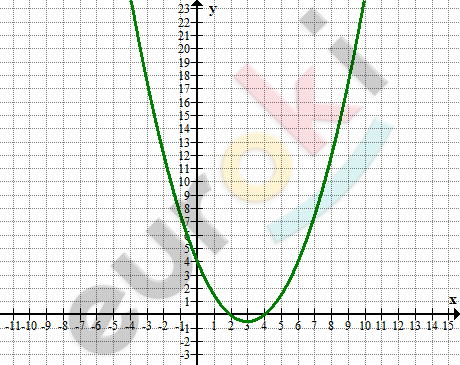
\[E(y) = \lbrack - 0,5;\ + \infty).\]
\[При\ x \in ( - \infty;3)\ функция\ \]
\[убывает\ и\ при\ x \in (3; + \infty)\ \]
\[возрастает.\]
\[y < 0\ \ при\ x \in (2;4)\ и\ y > 0\ \ \]
\[при\ \ x \in ( - \infty;2) \cup (4; + \infty).\]
\[\textbf{в)}\ y = 4 - 0,5x²\]
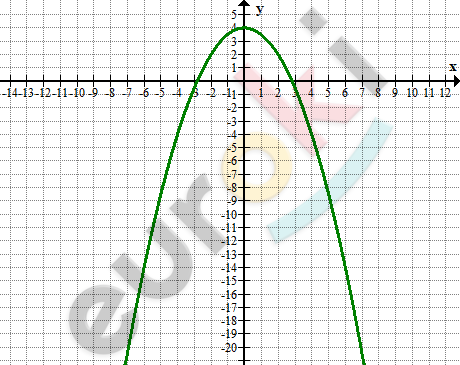
\[E(y) = ( - \infty;4\rbrack\]
\[Функция\ возрастает\ при\ \]
\[x \in ( - \infty;0);\]
\(убывает\ при\ x \in (0; + \infty).\)
\[\textbf{г)}\ y = 6x - 2x²\]
\[x_{b} = - \frac{b}{2a} = - \frac{6}{- 4} = \frac{3}{2};\]
\[y_{b} = 6 \cdot \frac{3}{2} - 2 \cdot \frac{9}{4} = 4,5;\]
\[6x - 2x^{2} = 0\]
\[2x(3 - x) = 0\]
\[x_{1} = 0\ \ и\ \ \ x_{2} = 3;\]
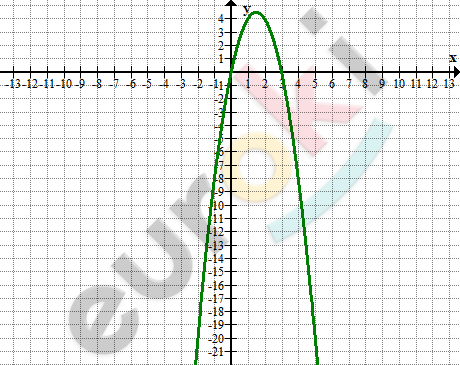
\[E(y) = ( - \infty;4,5\rbrack\]
\[y > 0\ \ при\ \ x \in (0;\ 3)\ и\ \ \]
\[y < 0\ \ \ при\ \]
\[\ x \in ( - \infty;0) \cup (3; + \infty);\]
\[Функция\ возрастает\ при\ \]
\[x \in ( - \infty;1,5)\ \ и\ \]
\[убывает\ \ (1,5; + \infty).\]
\[\textbf{д)}\ y = (2x - 7)(x + 1)\]
\[y = 2x^{2} - 5x - 7\]
\[x_{b} = - \frac{- 5}{4} = \frac{5}{4} = 1,25;\]
\[y_{b} = 2 \cdot \frac{25}{4} - 5 \cdot \frac{5}{4} - 7 =\]
\[= - 10,125;\]
\[x_{1} = - 1\ \ \ и\ \ \ x_{2} = 3,5 \Longrightarrow\]
\[\Longrightarrow нули\ функции;\]
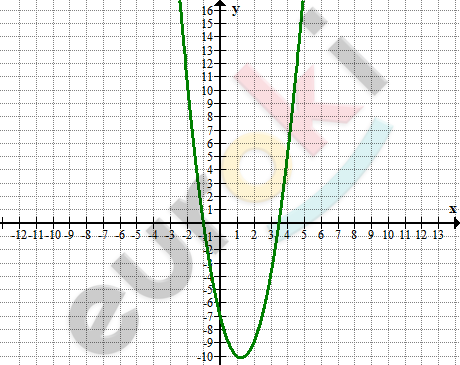
\[E(y) = \lbrack - 10,125;\ + \infty).\]
\[При\ x \in ( - \infty;1,25)\ функция\ \]
\[убывает\ и\ при\ x \in (1,25; + \infty)\ \]
\[возрастает.\]
\[y < 0\ \ при\ x \in ( - 1;3,5)\ и\ y > 0\ \ \]
\[при\ \ x \in ( - \infty; - 1) \cup (3,5; + \infty).\]
\[\textbf{е)}\ y = (2 - x)(x + 6)\]
\[y = - x^{2} - 4x + 12\]
\[x_{b} = - \frac{- 4}{- 2} = - 2,\ \ y_{b} = 16;\]
\[x_{1} = 2\ \ и\ \ x_{2} = - 2 \Longrightarrow\]
\[\Longrightarrow нули\ функции;\]
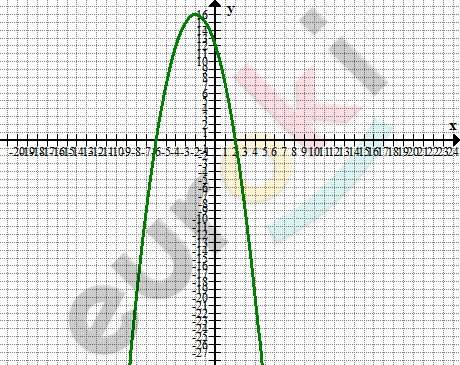
\[E(y) = ( - \infty;16\rbrack\]
\[y > 0\ \ при\ \ x \in ( - 6;\ - 2)\ и\ \ \]
\[y < 0\ \ \ при\ \ \]
\[x \in ( - \infty; - 6) \cup (2; + \infty);\]
\[Функция\ возрастает\ при\ \]
\[x \in ( - \infty; - 2)\ \ и\ \]
\[убывает\ \ ( - 2; + \infty).\]
