Решебник по алгебре 9 класс Мерзляк Задание 850

 

\[\boxed{\mathbf{850\ (850).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1){\ 2}^{- n},\ 2^{- 2n},2^{- 3n},2^{- 4n},\ldots\]

\[b_{1} \cdot b_{4} = b_{2} \cdot b_{3}\ \]

\[2^{- n} \cdot 2^{- 4n} = 2^{- 2n} \cdot 2^{- 3n}\text{\ \ }\]

\[\ 2^{- 5n} = 2^{- 5n} \Longrightarrow является;\]

\[q = \frac{2^{- 2n}}{2^{- n}} = 2^{- n}.\]

\[2)\ 2^{n},\ 2^{n^{2}},\ 2^{n^{3}},\ 2^{n^{4}},\ldots\]

\[b_{1} \cdot b_{4} = b_{2} \cdot b_{3}\ \]

\[2^{n} \cdot 2^{n^{4}} = 2^{n²} \cdot 2^{n³}\]

\[2^{{n + n}^{4}} \neq 2^{n^{2} + n^{3}} \Longrightarrow не\ является;\]

\[3)\ 2^{n},\ 2^{n + 1},\ 2^{n + 2},\ 2^{n + 3},\ldots\]

\[b_{1} \cdot b_{4} = b_{2} \cdot b_{3}\text{\ \ }\]

\[2^{n} \cdot 2^{n + 3} = 2^{n + 1} \cdot 2^{n + 2}\]

\[2^{2n + 3} = 2^{2n + 3} \Longrightarrow является;\]

\[q = \frac{2^{n + 1}}{2^{n}} = 2^{1} = 2.\]

\[\boxed{\mathbf{850.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\ a,\ b,\ c;\ \ b = a + d,\]

\[\ \ c = a + 2d,\]

\[\text{\ \ }то\ \ \ ac = a \cdot (a + 2d).\]

\[R = \frac{\text{abc}}{4S} - радиус\ описанной\ \]

\[окружности;\]

\[r = \frac{S}{p} - радиус\ вписанной\]

\[\ окружности.\]

\[6Rr = 6 \cdot \frac{\text{abc}}{4S} \cdot \frac{S}{p} = \frac{6}{4} \cdot \frac{\text{abc}}{p} =\]

\[= \frac{3}{2} \cdot \frac{\text{abc}}{p} =\]

\[= \frac{3a(a + d)(a + 2d)}{\frac{2 \cdot (a + b + c)}{2}} =\]

\[= \frac{3a(a + d)(a + 2d)}{a + a + d + a + 2d} =\]

\[= \frac{3a(a + d)(a + 2d)}{3a + 3d} =\]

\[= \frac{3a(a + d)(a + 2d)}{3 \cdot (a + d)} =\]

\[= a(a + 2d) \Longrightarrow \ ac = 6Rr.\]

\[2)\ b = a + d;\ \ c = a + 2d,\ \]

\[По\ т.\ Пифагора\ a² + b² = c²\]

\[a^{2} + (a + d)^{2} = (a + 2d)^{2}\]

\[a^{2} + a^{2} + 2ad + d^{2} =\]

\[= a^{2} + 4ad + 4d^{2}\]

\[3d^{2} + 2ad - a^{2} = 0\]

\[D = 4a^{2} + 12a^{2} = 16a^{2}\]

\[d = \frac{- 2a + 4a}{6} = \frac{a}{3}\]

\[d = \frac{- 2a - 4a}{6} =\]

\[= - a\ (не\ удовлетворяет)\]

\[d = \frac{a}{3},\ \ тогда\ \ b = a + d =\]

\[= a + \frac{a}{3} = \frac{4}{3}a\]

\[c = a + 2d = a + \frac{2a}{3} = \frac{5a}{3}\]

\[r = \frac{a + b - c}{2} = \frac{a + \frac{4}{3}a - \frac{5}{3}a}{2} =\]

\[= \frac{\frac{2}{3}a}{2} = \frac{a}{3} \Longrightarrow \ r = d = \frac{a}{3}.\]

\[3)\ По\ т.\ косинусов:(a + 2d)^{2} =\]

\[= a^{2} + (a + d)^{2}\]

\[- - 2a(a + d) \cdot cos120{^\circ}.\]

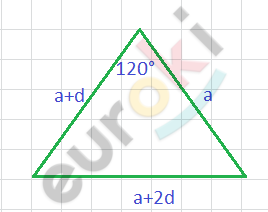
\[a^{2} + 4ad + 4d^{2} = a^{2} + a^{2} +\]

\[+ 2ad + d^{2} - 2a(a + d) \cdot \left( - \frac{1}{2} \right)\]

\[a^{2} + 4ad + 4d^{2} = 2a^{2} +\]

\[+ 2ad + d^{2} + a^{2} + ad\]

\[3a^{2} + ad - 2a^{2} = 0\]

\[D = a^{2} + 24a^{2} = 25a^{2}\]

\[d = \frac{- a + 5a}{6} = \frac{2}{3}a\]

\[d = \frac{- a - 5a}{6} =\]

\[= - a\ (не\ удовлетворяет).\]

\[d = \frac{2}{3}a,\ \ то\ \ \ a + d = a +\]

\[+ \frac{2}{3}a = \frac{5}{3}a,\]

\[\ \ a + 2d = a + \frac{4}{3}a = \frac{7}{3}a\]

\[Тогда\ \ a\ :\frac{5}{3}\text{a\ }:\frac{7}{3}a = 3\ :5\ :7.\]