Решебник по алгебре 9 класс Мерзляк Задание 725

 

\[\boxed{\mathbf{725\ (725).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\ a_{1} = 11,4;\ \ \ \ d = 0,6;\ \ \ \]

\[a_{n} = 20,4\]

\[a_{n} = a_{1} + d(n - 1)\ \]

\[\ 20,4 = 11,4 + 0,6 \cdot (n - 1)\]

\[20,4 = 11,4 + 0,6n - 0,6\]

\[0,6n = 9,6\]

\[n = 16\]

\[20,4\ является\ членом\ \]

\[арифметической\ \]

\[прогрессии \Longrightarrow \ \ n = 16.\]

\[2)\ a_{1} = 8;\ \ \ \ d = 1,4;\ \ \ a_{n} = 38\]

\[a_{n} = a_{1} + d(n - 1)\]

\[38 = 8 + 1,4 \cdot (n - 1)\]

\[38 = 8 + 1,4n - 1,4\]

\[1,4n = 31,4\]

\[n = \frac{31,4}{1,4}\]

\[n \approx 22,4\]

\[Тогда\ 8\ не\ является\ членом\]

\[\ арифметической\ прогрессии.\]

\[Ответ:1)\ да;\ \ n = 16;\ \ 2)\ нет.\]

\[\boxed{\mathbf{725.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

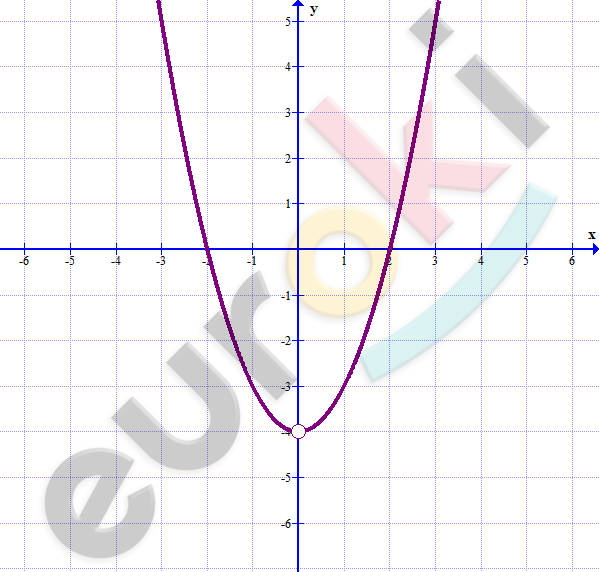
\[1)\ y = \frac{x^{3}}{x} - 4 = x^{2} - 4;\ \ \ x \neq 0\]

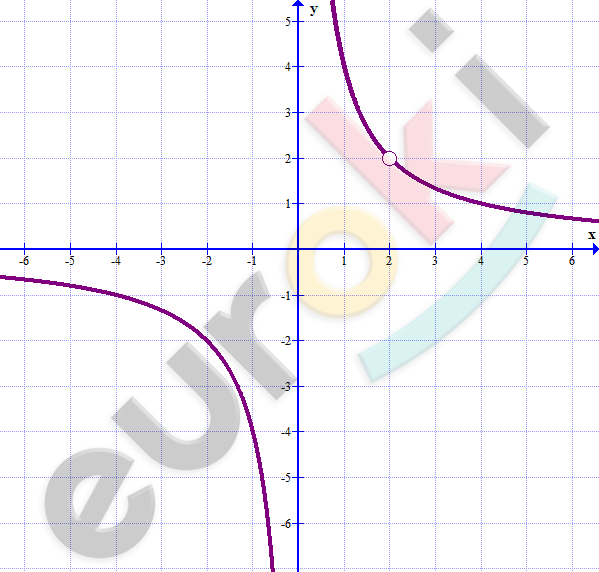
\[2)\ y = \frac{4x - 8}{x^{2} - 2x} = \frac{4(x - 2)}{x(x - 2)} =\]

\[= \frac{4}{x};\ \ x \neq 0;\ \ x \neq 2\]