Решебник по алгебре 9 класс Мерзляк Задание 542

 

\[\boxed{\mathbf{542\ (}\mathbf{с}\mathbf{).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ на\text{\ x}\% - была\ снижена\ \]

\[цена\ в\ первый\ раз,\ тогда\ \]

\[2x\% - снижена\ \]

\[во\ второй\ раз.\ По\ условию\ \]

\[известно,\ что\ стоило\ одеяло\]

\[\ 600\ руб.,\ а\ стало\]

\[стоить\ 432\ руб.\ Значит,\ \]

\[\left( 600 - \frac{600x}{100} \right)\ руб. - цена\ после\ \]

\[первого\ снижения.\]

\[Составляем\ уравнение:\]

\[600 - \frac{600x}{100} -\]

\[- \frac{\left( 600 - \frac{600x}{100} \right) \cdot 2x}{100} = 432\]

\[600 - 6x - \frac{(600 - 6x)x}{50} = 432\]

\[(600 - 6x)\left( 1 - \frac{x}{50} \right) = 432\]

\[6 \cdot (100 - x)\left( \frac{50 - x}{50} \right) = 432\]

\[(100 - x)(50 - x) = 3600\]

\[- 100x + 5000 - 50x + x^{2} -\]

\[- 3600 = 0\]

\[x^{2} - 150x + 1400 = 0\]

\[x_{1} + x_{2} = 150,\ \ \]

\[x_{1}x_{2} = 1400,\ \ \]

\[x_{1} = 140\ (не\ удовлетворяет)\]

\[x_{2} = 10\]

\[На\ 10\%\ была\ снижена\ цена\ \]

\[в\ первый\ раз.\]

\[2 \cdot 10\% = 20\% - на\ столько\ \]

\[цена\ была\ снижена\ во\ \]

\[второй\ раз.\]

\[Ответ:на\ 10\%;на\ 20\%.\]

\[\boxed{\mathbf{542.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\ y = \frac{\sqrt{2 - x}}{x + 2}\]

\[\left\{ \begin{matrix} 2 - x \geq 0 \\ x + 2 \neq 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x \leq 2\ \ \ \\ x \neq - 2 \\ \end{matrix} \right.\ \]

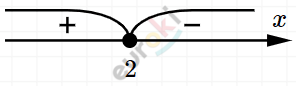
\[Ответ:x \in ( - \infty;\ - 2) \cup ( - 2;2\rbrack.\]

\[2)\ y = \frac{\sqrt{6 - 5x - x^{2}}}{x - 1}\]

\[\left\{ \begin{matrix} 6 - 5x - x^{2} \geq 0 \\ x - 1 \neq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\text{\ \ }\left\{ \begin{matrix} x² + 5x - 6 \leq 0 \\ x \neq 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[x^{2} + 5x - 6 = 0\]

\[x_{1} + x_{2} = - 5,\ \ x_{1} = - 6\]

\[x_{1}x_{2} = - 6,\ \ x_{2} = 1\]

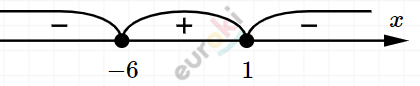
\[Ответ:x \in \lbrack - 6;1).\]