Решебник по алгебре 9 класс Мерзляк Задание 538

 

\[\boxed{\mathbf{538\ (538).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\% - новая\ \]

\[производительность,\ по\ \]

\[условию\ известно,\ что\ \]

\[производительность\ рабочего\ \]

\[была\ \frac{1}{20},\ а\ стала\ \frac{1}{8}.\]

\[Составляем\ уравнение:\]

\[\frac{1}{20}\ :\frac{1}{8} = \frac{100}{x}\]

\[\frac{8}{20} = \frac{100}{x}\]

\[8x = 2000\]

\[x = 250\ \% - новая\ \]

\[производительность.\]

\[250\% - 100\% = 150\% - на\]

\[\ столько\ выросла\]

\[\ производительность.\]

\[Ответ:на\ 150\%.\]

\[\boxed{\mathbf{538.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[b_{n} = - n^{2} + 15n - 20\]

\[- n^{2} + 15n - 20 > 16\ \ \]

\[- n^{2} + 15n - 36 > 0\]

\[n^{2} - 15n + 36 < 0\]

\[n_{1} + n_{2} = 15,\ \ n_{1} = 12\]

\[n_{1}n_{2} = 36,\ \ n_{2} = 3\]

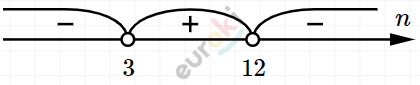
\[Тогда\ 4;5;6;7;8;9;10;\]

\[11 - 8\ членов.\]

\[Ответ:8.\]