Решебник по алгебре 9 класс Мерзляк Задание 510

 

\[\boxed{\mathbf{510\ (510).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x - бригад\ было\ всего,\ а\ \]

\[y - человек\ в\ каждой\ \]

\[бригаде.\ Тогда\ \]

\[2x\ штук - надо\ комплектов\ на\]

\[\ каждую\ бригаду.\ \ Значит,\]

\[\ x + 20 = 2y.\]

\[Известно,\ что\ если\ бригад\ \]

\[(x + 4),\ то\ каждой\ бригаде\]

\[\ выдавали\ бы\ по\]

\[\ 12\ комплектов,\ то\ есть,\ 12 \cdot\]

\[\cdot (x + 4)\ штук.\ Тогда\ одежды\]

\[\ на\ всех\ бы\ не\]

\[хватило.\ Получаем\ \]

\[неравенство:12 \cdot (x + 4) > 2xy.\]

\[Составляем\ систему\]

\[\ неравенств:\]

\[\left\{ \begin{matrix} 12 \cdot (x + 4) > 2xy \\ x + 20 = 2y \\ \end{matrix} \right.\ \ \]

\[12 \cdot (x + 4) > (x + 20) \cdot x\]

\[12x + 48 - x^{2} - 20x > 0\]

\[x^{2} + 8x - 48 < 0\]

\[x_{1} + x_{2} = - 8,\ \ x_{1} = - 12\]

\[x_{1}x_{2} = - 48,\ \ x_{2} = 4\]

\[Удовлетворяют\ \ x = 1;x = 2;\]

\[x = 3,\ так\ как\ отрицательного\ \]

\[числа\ бригад\]

\[быть\ не\ может.\]

\[Так\ как\ x + 20 = 2y,\ то\ \]

\[x = 20y - 20 \Longrightarrow четное\ число.\ \]

\[Следовательно,\ \]

\[x = 2 - бригады\ было\ всего.\]

\[2y - 20 = 2\ \ \]

\[y = 11\ (человек) - в\ каждой\ \]

\[бригаде.\]

\[2 \cdot 11 \cdot 2 =\]

\[= 44\ (комплекта) - было\ на\]

\[\ складе.\]

\[Ответ:44\ комплекта.\]

\[\boxed{\text{510.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)y = \frac{5}{\sqrt{x^{2} - 4x - 12}} + \sqrt{x + 1}\]

\[\left\{ \begin{matrix} x^{2} - 4x - 12 > 0 \\ x + 1 \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1)\ x^{2} - 4x - 12 > 0\]

\(x_{1} + x_{2} = 4,\ \ \ \ \ \ \ \ \ \ \ x_{1} = 6\)

\[x_{1}x_{2} = - 12,\ \ x_{2} = - 2\]

\[2)\ x + 1 \geq 0\]

\[x \geq - 1\]

\[\left\{ \begin{matrix} (x - 6)(x + 2) > 0 \\ x \geq - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:x \in (6;\ + \infty).\]

\[2)\ y = \frac{x - 3}{\sqrt{18 + 3x - x^{2}}} + \frac{8}{x - 5}\]

\[\left\{ \begin{matrix} 18 + 3x - x^{2} > 0 \\ x - 5 \neq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1)\ - x^{2} + 3x + 18 > 0\]

\(x_{1} + x_{2} = 3,\ \ \ \ \ \ \ \ \ \ \ x_{1} = 6\)

\[x_{1}x_{2} = - 18,\ \ x_{2} = - 3\]

\[2)\ x - 5 \neq 0\]

\[x \neq 5\]

\[\left\{ \begin{matrix} (x - 6)(x + 3) > 0 \\ x \neq 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:x \in ( - 3;5) \cup (5;6).\]

\[3)\ y = \sqrt{x^{2} - 5x - 14} - \frac{9}{x^{2} - 81}\]

\[\left\{ \begin{matrix} x^{2} - 5x - 14 \geq 0 \\ x^{2} - 81 \neq 0\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1)\ x^{2} - 5x - 14 \geq 0\]

\(x_{1} + x_{2} = 5,\ \ \ \ \ \ \ \ \ \ \ x_{1} = 7\)

\[x_{1}x_{2} = - 14,\ \ x_{2} = - 2\]

\[2)\ x^{2} - 81 \neq 0\]

\[x^{2} \neq 81\]

\[x \neq \pm 9\]

\[\left\{ \begin{matrix} (x - 7)(x + 2) \geq 0 \\ x \neq 9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x \neq - 9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

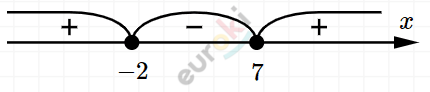
\[Ответ:x \in ( - \infty; - 9) \cup\]

\[\cup ( - 9;\ - 2\rbrack \cup \lbrack 7;\ 9) \cup (9;\ + \infty).\]

\[4)\ y = \frac{1}{\sqrt{6 - 7x - 3x^{2}}} + \frac{2}{\sqrt{x + 1}}\]

\[\left\{ \begin{matrix} 6 - 7x - 3x^{2} > 0 \\ x + 1 > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1)\ - 3x^{2} - 7x + 6 > 0\]

\[D = 121\]

\[x_{1,2} = \frac{7 \pm 11}{- 6}\]

\[x = - 3;\ \ \ x = \frac{2}{3}\]

\[2)\ x + 1 > 0\]

\[x > - 1\]

\[\left\{ \begin{matrix} (x + 3)\left( x - \frac{2}{3} \right) > 0 \\ x > - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

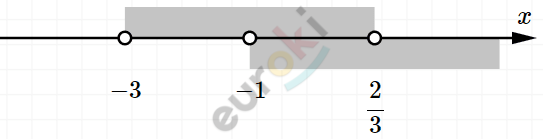
\[Ответ:x \in \left( - 1;\frac{2}{3} \right)\text{.\ }\]