Решебник по алгебре 9 класс Мерзляк Задание 504

 

\[\boxed{\mathbf{504\ (504).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[500\ м^{3} = 500\ 000\ л;\ \]

\[300\ \frac{л}{мин} = 18\ 000\ \frac{л}{ч};\ \ \]

\[12\ ч\ 30\ мин = 12,5\ ч.\]

\[Пусть\ \text{x\ }\frac{л}{ч} - скорость\ подачи\ \]

\[воды\ через\ первую\ трубу,\ \]

\[\text{y\ }\frac{л}{ч} -\]

\[скорость\ через\ вторую\ трубу;\]

\[z\frac{л}{ч} - скорость\ через\]

\[\ третью\ трубу.\ \]

\[Тогда\ t\ ч - время,\ которое\]

\[\ была\ открыта\ 1\ труба,\ а\]

\[\ 2t\ ч - время,\ которое\]

\[были\ открыты\ 2\ и\ 3\ труба.\]

\[По\ условию\ известно,\ что\]

\[\ емкость\ бака\ 500\ 000\ л,\ а\ \]

\[через\ первую\]

\[трубу\ вода\ поступала\ со\]

\[\ скоростью\ 18\ 000\ \frac{л}{ч}\text{.\ }\]

\[Получаем\ уравнение\ \]

\[18\ 000t +\]

\[+ (y + z) \cdot 2t = 500\ 000.\]

\[По\ условию\ также\ известно,\ \]

\[что\ если\ были\ бы\ открыты\ \]

\[2\ и\ 3\ трубы\ 12,5\ ч;\]

\[то\ через\ них\ подали\ бы\ воды,\]

\[\ сколько\ было\ подано\ из\ \]

\[первой\ трубы.\]

\[Получаем\ уравнение:\]

\[(y + z) \cdot 12,5 = 18\ \ 000t.\]

\[Составляем\ систему\]

\[\ уравнений:\]

\[\left\{ \begin{matrix} 18000t + (y + z) \cdot 2t = 500000 \\ (y + z) \cdot 12,5 = 18000t \\ \end{matrix} \right.\ \text{\ \ \ }\ \]

\[\ \left\{ \begin{matrix} 18000t + (y + z) \cdot 2t = 500000 \\ y + z = \frac{18000t}{12,5} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 18000t + (y + z) \cdot 2t = 500000 \\ y + z = 1440t \\ \end{matrix} \right.\ \]

\[18000t + (1440t) \cdot 2t =\]

\[= 500000\]

\[2880t^{2} + 18000t -\]

\[- 500000 = 0\ \ \ |\ :80\]

\[36t^{2} + 225t - 6250 = 0\]

\[D = 950\ 625\]

\[t_{1} = \frac{- 225 + 975}{72} = \frac{750}{72}\]

\[t_{2} = \frac{- 225 - 975}{72} =\]

\[= - \frac{1200}{72} - не\ удовлетворяет.\]

\[\frac{750}{72}\ ч = 10\frac{32}{72}\ ч = 10\frac{5}{12}\ ч =\]

\[= 10\ ч\ 25\ мин - была\ открыта\ \]

\[первая\ труба.\]

\[Ответ:10\ ч\ 25\ мин.\]

\[\boxed{\text{504.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[1)\ x^{2} - 2x - 15 > 0\ \ \]

\(x_{1} + x_{2} = 2,\ \ \ \ \ \ \ \ \ \ \ x_{1} = 5\)

\[x_{1}x_{2} = - 15,\ \ x_{2} = - 3\]

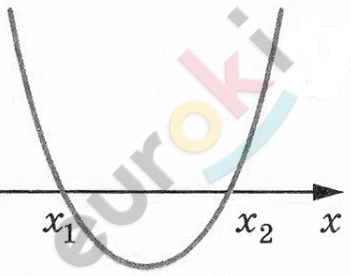
\[x \in ( - \infty;\ - 3) \cup (5;\ + \infty).\]

\[x^{2} - 2x - 15 \geq 0\]

\[x \in ( - \infty; - 3\rbrack \cup \lbrack 5;\ + \infty).\]

\[Ответ:не\ равносильны.\]

\[2)\ \frac{1}{x^{2} - x - 20} < 0\ \ \ \ и\ \ \ \ \]

\[\frac{1}{x^{2} - x - 20} \leq 0\]

\[\frac{1}{x^{2} - x - 20} \leq 0 - дробь\ \]

\[принимать\ значение\ 0\ не\ \]

\[может,\ поэтому\]

\[\Longrightarrow \frac{1}{x^{2} - x - 20} < 0\]

\[Ответ:равносильны.\]

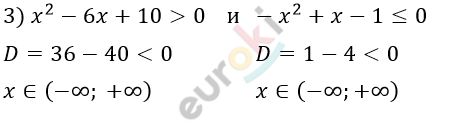
\[Ответ:равносильны.\]