Решебник по алгебре 9 класс Мерзляк Задание 503
Задание 503



\[\boxed{\mathbf{503\ (503).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]
\[Пусть\ x\ \frac{км}{ч} - скорость\ \]
\[товарного\ поезда,\ а\ y\]
\[\ \frac{км}{ч} - скорость\]
\[пассажирского.\ Тогда\ 4x\]
\[\ км - прошел\ товарный\ поезд\]
\[\ за\ 4\ часа,\ от\]
\[C\ до\ B,\ а\ 6y\ км - прошел\ \]
\[пассажирский\ поезд\ за\ 6\ ч\]
\[\ от\ C\ до\ A.\]
\[Если\ t - время\ встречи\ в\ \]
\[пункте\ C,\ а\ по\ условию\ \]
\[известно,\ что\ пассажирский\ \]
\[поезд\ выехал\ на\ 5\ часов\ \]
\[позже,\ то\ 5x\ км - проехал\ \]
\[товарный\ поезд\ до\]
\[того,\ как\ выехал\ пассажирский,\ \]
\[и\ \text{xt\ }\ км - проехал\ до\ встречи\]
\[\ в\ пункте\ C,\ \]
\[а\ \text{yt}\ км - проехал\ \]
\[пассажирский\ поезд\ до\]
\[\ встречи\ с\ товарным.\]
\[Составляем\ систему\ \]
\[уравнений:\]
\[\left\{ \begin{matrix} 4x = yt\ \ \ \ \ \ \ \ \ \\ 6y = 5x + xt \\ 4x + 6y = a \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} t = \frac{4x}{y}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 6y = 5x + \frac{4x^{2}}{y}\ \ \ |\ \cdot y \\ 4x + 6y = a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]
\[a - расстояние\ между\ \]
\[пунктами.\]
\[6y^{2} - 5xy - 4x^{2} = 0\]
\[D = 25x^{2} + 96x^{2} = 121x^{2}\]
\[y_{1} = \frac{5x + 11x}{12} = \frac{4x}{3}\]
\[y_{2} = \frac{5x - 11x}{12} = - \frac{x}{2} - не\]
\[\ удовлетворяет.\]
\[\left\{ \begin{matrix} t = \frac{4x}{y}\text{\ \ \ \ \ \ \ \ \ \ } \\ y = \frac{4x}{3}\text{\ \ \ \ \ \ \ \ \ \ \ } \\ 4x + 6y = a \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} y = \frac{4x}{3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 4x + \frac{24x}{3} = a \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\text{\ \ }\left\{ \begin{matrix} y = \frac{4x}{3}\text{\ \ \ \ \ \ \ \ \ } \\ 4x + 8x = a \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} y = \frac{4x}{3} \\ 12x = a \\ \end{matrix} \right.\ \ \ \ \ \ \ \ и\ \ \ \ \ \ \ \ \]
\[\left\{ \begin{matrix} x = \frac{3}{4}y \\ 12 \cdot \frac{3}{4}y = a \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = \frac{3}{4}y \\ 9y = a \\ \end{matrix} \right.\ \]
\[\frac{a}{x} = \frac{12x}{x} = 12\ (ч) - время,\ за\ \]
\[которое\ преодолеет\]
\[\ расстояние\ товарный\]
\[поезд.\]
\[\frac{a}{y} = \frac{9y}{y} = 9\ (ч) - время,\ за\]
\[\ которое\ преодолеет\ \]
\[расстояние\ пассажирский\]
\[поезд.\]
\[Ответ:12\ ч;\ 9\ ч.\]

\[\boxed{\text{503.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ \sqrt{2x^{2} - 9x - 18}\]
\[2x^{2} - 9x - 18 \geq 0\]
\[D = 81 + 144 = 225\]
\[x_{1,2} = \frac{9 \pm 15}{4}\]
\[x = - 1,5;\ \ x = 6\]
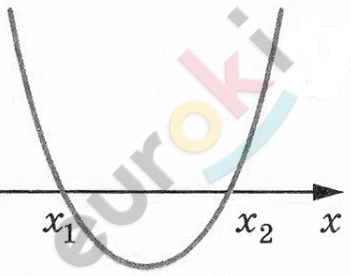
\[Ответ:x \in ( - \infty; - 1,5\rbrack \cup \lbrack 6;\ + \infty).\]
\[2)\ \frac{1}{\sqrt{15 + 2x - x^{2}}}\]
\[15 + 2x - x^{2} > 0\]
\[- x^{2} + 2x + 15 > 0\]
\[x_{1} + x_{2} = 2,\ \ x_{1} = - 3\]
\[x_{1}x_{2} = - 15,\ \ x_{2} = 5\]
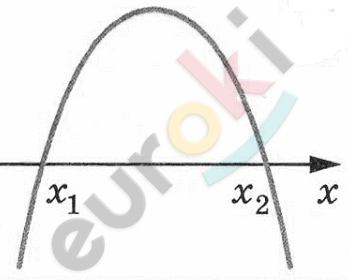
\[Ответ:x \in ( - 3;5).\]




