Решебник по алгебре 9 класс Мерзляк Задание 499

 

\[\boxed{\text{499\ (499).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\frac{км}{ч} - скорость\ по\ \]

\[течению,\ а\ y\frac{км}{ч} - скорость\ \]

\[против\]

\[течения.\ Скорость\ лодки\ в\ \]

\[стоячей\ воде\ равна\ \]

\[собственной\ скорости\]

\[лодки.\ По\ условию\ известно,\]

\[\ что\ лодка\ проходит\ 34\ км\ по\ \]

\[течению\]

\[и\ 39\ км\ против\ течения\ за\ то\ \]

\[же\ время,\ что\ 75\ км\ в\ стоячей\ \]

\[воде.\]

\[Составляем\ уравнение:\]

\[\frac{34}{x} + \frac{39}{y} = \frac{75}{a},\ где\ a -\]

\[собственная\ скорость\ лодки\]

\[Запишем\ \ x = a + b,\ y = a - b,\ \]

\[где\ a - собственная\ скорость\]

\[\ лодки,\]

\[b - скорость\ течения.\]

\[\frac{34}{a + b} + \frac{39}{a - b} = \frac{75}{a}\]

\[\frac{34a - 34b + 39a + 39b}{(a + b)(a - b)} = \frac{75}{a}\]

\[\frac{73a + 5b}{a^{2} - b^{2}} = \frac{75}{a}\]

\[\frac{(73a + 5b)a - 75\left( a^{2} - b^{2} \right)}{\left( a^{2} - b^{2} \right)a} = 0\]

\[73a^{2} + 5ab - 75a^{2} + 75b^{2} = 0\]

\[2a^{2} - 5ab - 75b^{2} = 0\ \ \ \ \ \ \ \ | \cdot \frac{1}{b^{2}}\]

\[2 \cdot \left( \frac{a}{b} \right)^{2} - 5\frac{a}{b} - 75 = 0\]

\[пусть\frac{a}{b} = t,\ то\ 2t^{2} -\]

\[- 5t - 75 = 0\]

\[D = 25 + 8 \cdot 75 = 625\]

\[t_{1} = \frac{5 - 25}{4} = - 5 -\]

\[не\ удовлетворяет.\]

\[t_{2} = \frac{5 + 25}{4} = \frac{15}{2}.\]

\[Ответ:соотношение\ скорости\]

\[\ лодки\ в\ стоячей\ воде\ к\ \]

\[скорости\ течения\]

\[равно\ 15\ :2.\ \]

\[\boxed{\text{499.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

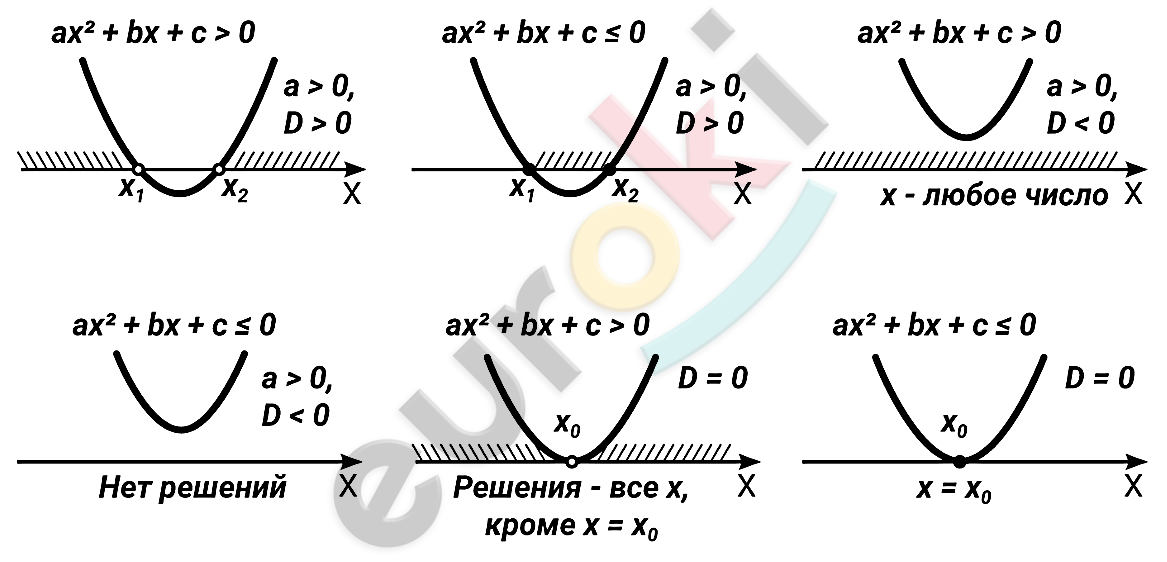
Пояснение.

\[Решение\ квадратных\ \]

\[неравенств.\]

Решение.

\[1)\ 42 - x^{2} - x > 0\]

\[- x^{2} - x + 42 > 0\]

\[x_{1} + x_{2} = - 1,\ \ x_{1} = - 7\]

\[x_{1}x_{2} = - 42,\ \ x_{2} = 6\]

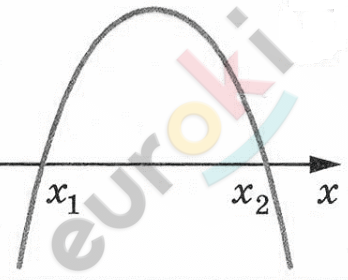
\[Ответ:\ x = - 6.\]

\[2)\ 2x^{2} - 3x - 20 < 0\]

\[D = 9 + 160 = 169\]

\[x_{1,2} = \frac{3 \pm 13}{4}\]

\[x = - 2,5;\ \ \ \ x = 4\]

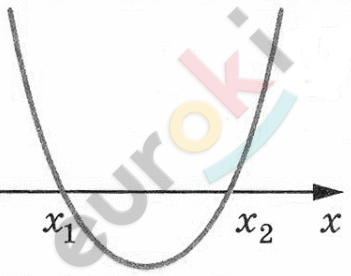
\[Ответ:\ x = - 2.\ \]