Решебник по алгебре 9 класс Мерзляк Задание 498

 

\[\boxed{\text{498\ (498).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ \frac{км}{ч}\ скорость\ по\ \]

\[течению,\ а\ y\ \frac{км}{ч} - против\ \]

\[течения,\ c\ км -\]

\[расстояние\ от\ пункта\ A\ до\ \]

\[пункта\ B.\ Тогда\ \frac{c}{x} = 3\ ч -\]

\[время\ теплохода\ в\ \]

\[пути\ по\ течению,\ а\ \frac{c}{y} = 4\ ч -\]

\[время\ в\ пути\ против\ течения.\]

\[Составляем\ систему\ уравнений:\]

\[\left\{ \begin{matrix} \frac{c}{x} = 3 \\ \frac{c}{y} = 4 \\ \end{matrix} \right.\ \]

\[пусть\ x = a + b,\ y = a - b,\ где\ \]

\[a - собственная\ скорость\ \]

\[плота,\]

\[а\ b - скорость\ течения.\]

\[\left\{ \begin{matrix} \frac{c}{a + b} = 3 \\ \frac{c}{a - b} = 4 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} a + b = \frac{c}{3} \\ a - b = \frac{c}{4} \\ \end{matrix} - \right.\ \]

\[\left\{ \begin{matrix} 2b = \frac{c}{12}\text{\ \ \ \ } \\ a - b = \frac{c}{4} \\ \end{matrix} \right.\ \]

\[2b = \frac{c}{12}\]

\[b = \frac{c}{24}\]

\[\frac{c}{24}\ \frac{км}{ч} - скорость\ течения\ \]

\[и\ скорость\ плота,\ тогда\]

\[\frac{c}{b} = \frac{c}{\frac{c}{24}} = 24\ ч - время,\ за\ \]

\[которое\ проплывет\ плот\]

\[\ расстояние\]

\[от\ A\ до\ B.\]

\[Ответ:24\ ч.\ \]

\[\boxed{\text{498.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

\[Решение\ квадратных\ \]

\[неравенств.\]

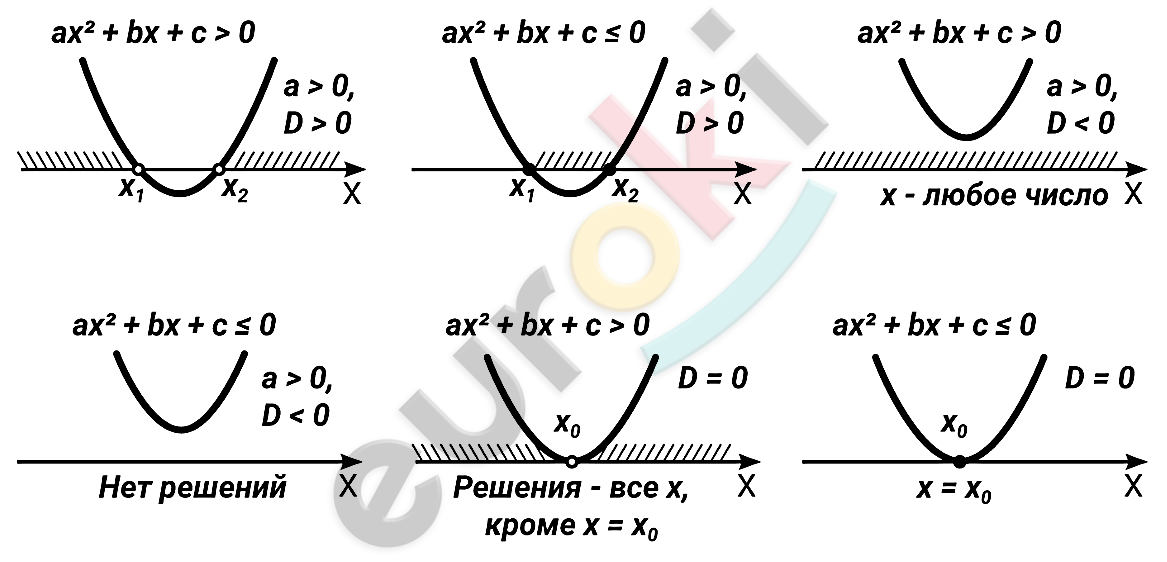
Решение.

\[1)\ 20 - 8x - x^{2} > 0\]

\[- x^{2} - 8x + 20 > 0\]

\[x_{1} + x_{2} = - 8,\ \ x_{1} = - 10\]

\[x_{1}x_{2} = - 20,\ \ x_{2} = 2\]

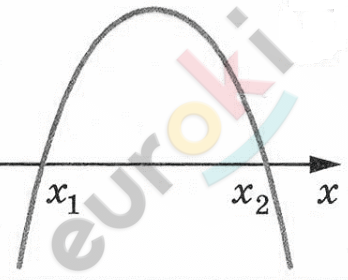
\[Ответ:11\ целых\ решений.\]

\[2)\ 4x^{2} - 15x - 4 < 0\]

\[D = 225 + 64 = 289\]

\[x_{1,2} = \frac{15 \pm 17}{8}\]

\[x = 4;\ \ \ x = - 0,25\]

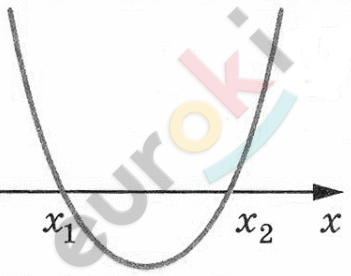
\[Ответ:4\ целых\ решения.\]