Решебник по алгебре 9 класс Мерзляк Задание 496
Задание 496



\[\boxed{\text{496\ (496).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Пусть\ x\ кг\ надо\ взять\ первого\ \]
\[сплава,\ а\ y\ кг - второго\ сплава,\ \]
\[тогда\]
\[\frac{5x}{7}\ кг - масса\ меди\ в\ первом\ \]
\[сплаве,\ а\ \frac{2x}{7}\ кг - масса\ цинка\ \]
\[в\ первом\]
\[сплаве.\ Значит,\ \frac{3y}{7}\ кг - масса\ \]
\[меди\ во\ втором\ сплаве,\ \]
\[а\frac{4y}{7}\ кг - масса\]
\[цинка\ во\ втором\ сплаве.\ \]
\[По\ условию\ известно,\ что\ в\ \]
\[полученном\ сплаве\]
\[равном\ 28\ кг\ содержание\ \]
\[меди\ и\ цинка\ поровну.\]
\[Составляем\ систему\ \]
\[уравнений:\]
\[\left\{ \begin{matrix} \frac{2}{7}x + \frac{4}{7}y = 14 \\ \frac{5}{7}x + \frac{3}{7}y = 14 \\ \end{matrix} - \right.\ \]
\[\left\{ \begin{matrix} \frac{1}{7}y - \frac{3}{7}x = 0 \\ \frac{2}{7}x + \frac{4}{7}y = 14 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = \frac{7}{3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{2y}{21} + \frac{4y}{7} = 14 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = \frac{7}{3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{14y}{21} = 14\ \ \ \ \ |\ :14 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = \frac{7}{3}\text{\ \ } \\ y = 21 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 7\ \ \\ y = 21 \\ \end{matrix} \right.\ \]
\[7\ кг - надо\ взять\ первого\ \]
\[сплава.\]
\[21\ кг - надо\ взять\ второго\ \]
\[сплава.\]
\[Ответ:7\ кг;21\ кг.\ \ \]

\[\boxed{\text{496.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
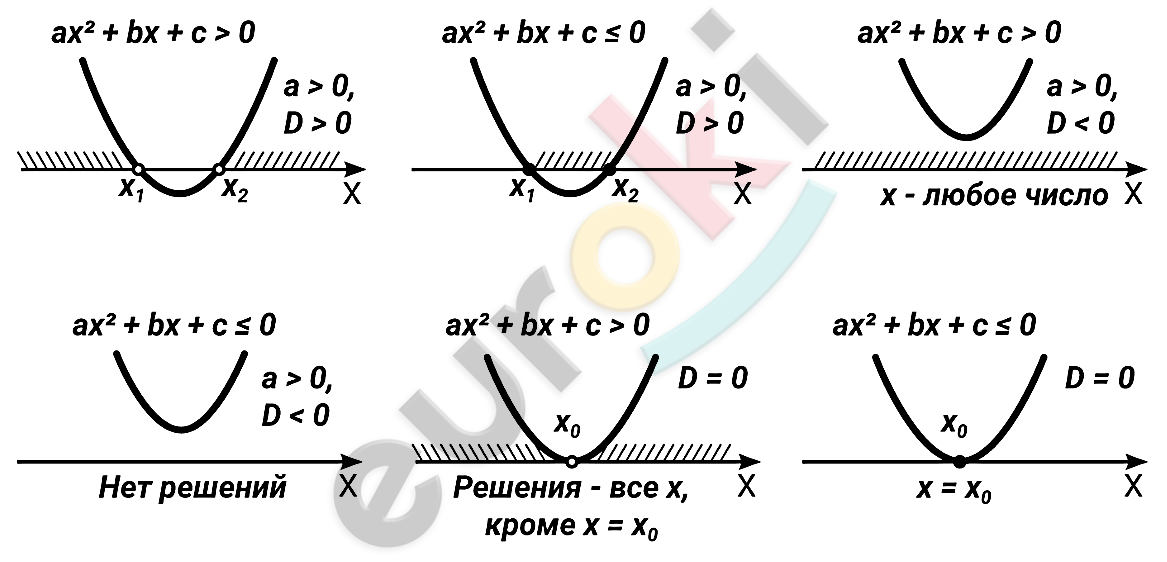
\[Решение\ квадратных\ \]
\[неравенств.\]
Решение.
\[\frac{3}{2}x^{2} - 7x + 1 < - \frac{1}{2}x^{2} - 4\ \ | \cdot 2\]
\[3x^{2} - 14x + 2 < - x^{2} - 8\]
\[3x^{2} + x^{2} - 14x + 2 + 8 < 0\]
\[4x^{2} - 14x + 10 < 0\ \ |\ \ :2\]
\[2x^{2} - 7x + 5 < 0\]
\[D = 49 - 40 = 9\]
\[x_{1,2} = \frac{7 \pm 3}{4}\]
\[x = 1;\ \ \ x = 2,5\]
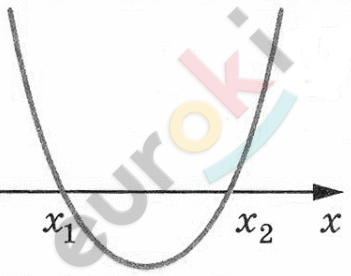
\[Ответ:x \in (1;2,5).\]




