Решебник по алгебре 9 класс Мерзляк Задание 495
Задание 495



\[\boxed{\text{495\ (495).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Пусть\ за\ x\ ч - вспахает\ поле\ \]
\[первый\ тракторист,\ \]
\[а\ за\ y\ ч - второй\]
\[тракторист.\ Тогда\ \frac{1}{x}\ поля\ \]
\[вспахает\ первый\ за\ 1\ час,\]
\[\ а\ \frac{6}{x}\ поля\ за\ 6\ ч,\]
\[а\ \frac{1}{y}\ поля\ вспахает\ второй\ \]
\[за\ 1\ ч,\ а\ \frac{6}{y}\ поля - за\ 6\ ч.\]
\[По\ условию\ известно,\ что\ за\ 6\ \]
\[часов\ оба\ тракториста\ могут\ \]
\[вспахать\]
\[поле,\ так\ же\ если\ \frac{4}{x}\ поля\ \]
\[вспахает\ первый\ тракторист,\ \]
\[\frac{9}{y}\ поля\ вспахает\]
\[второй\ тракторист,\ то\ поле\ \]
\[будет\ вспахано.\]
\[Составим\ систему\ уравнений:\]
\[\left\{ \begin{matrix} \frac{6}{x} + \frac{6}{y} = 1 \\ \frac{4}{x} + \frac{9}{y} = 1 \\ \end{matrix} - \right.\ \]
\[\left\{ \begin{matrix} \frac{2}{x} - \frac{3}{y} = 0 \\ \frac{6}{x} + \frac{6}{y} = 1\ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = \frac{2y}{3}\text{\ \ \ \ \ \ \ \ } \\ \frac{18}{2y} + \frac{6}{y} = 1 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{15}{y} = 1 \\ x = \frac{2y}{3} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} y = 15 \\ x = 10 \\ \end{matrix} \right.\ \]
\[10\ часов - \ вспахивает\ поле\ \]
\[первый\ тракторист;\]
\[15\ часов - вспахивает\ поле\ \]
\[второй\ тракторист.\]
\[Ответ:10\ ч;15\ ч.\ \]

\[\boxed{\text{495.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
\[Решение\ квадратных\ \]
\[неравенств.\]
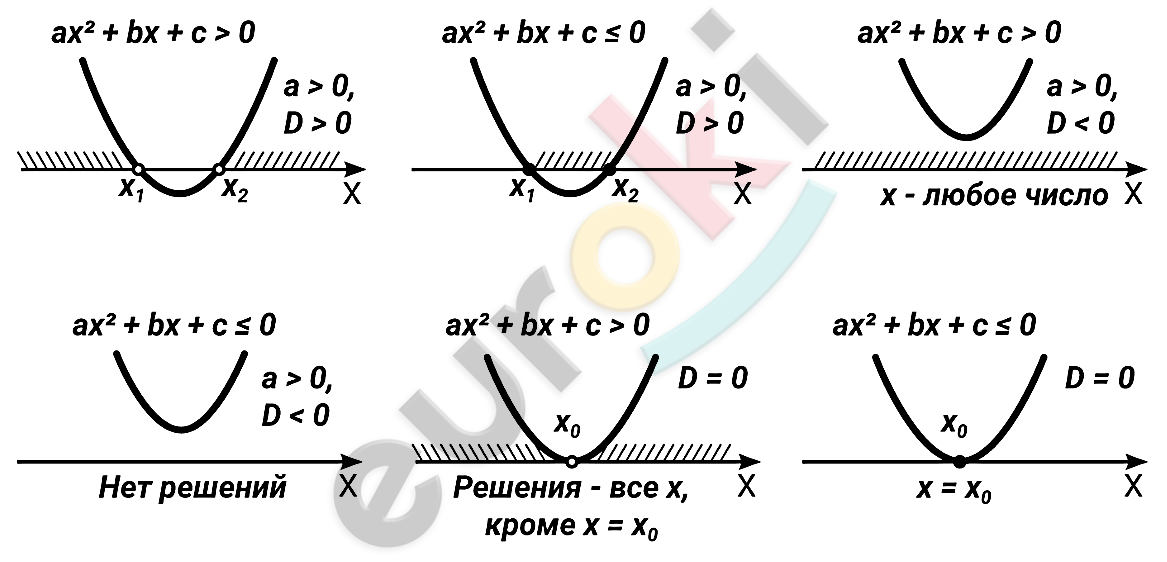
Решение.
\[- \frac{1}{2}x^{2} + \frac{3}{2}x + 9 > 2x - 1| \cdot ( - 2)\]
\[x^{2} - 3x - 18 + 4x - 2 < 0\]
\[x^{2} + x - 20 < 0\]
\[x_{1} + x_{2} = - 1,\ \ x_{1} = - 5\]
\[x_{1}x_{2} = - 20,\ \ x_{2} = 4\]
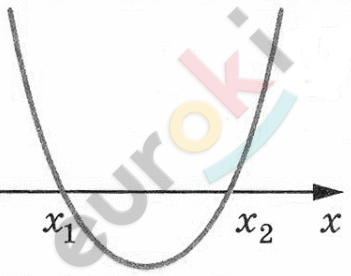
\[Ответ:x \in ( - 5;4).\]




