Решебник по алгебре 9 класс Мерзляк Задание 494

 

\[\boxed{\text{494\ (494).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ ч - требуется\ для\ \]

\[заполнения\ бассейна\ через\ \]

\[первую\ трубу,\]

\[а\ y\ ч - через\ вторую\ трубу.\]

\[\ Тогда\ \frac{1}{x} - заполняет\ первая\ \]

\[труба\ за\ 1\ ч,\]

\[а\ \frac{12}{x} - за\ 12\ ч,\ значит,\ \frac{1}{y} -\]

\[заполняет\ вторая\ труба\ за\ \]

\[1\ ч,\ а\ \frac{12}{y} - за\ 12\ ч.\]

\[По\ условию\ известно,\ что\ две\ \]

\[трубы\ заполнят\ бассейн\ за\ \]

\[12\ ч,\ водой\ \]

\[будет\ заполнена\ \frac{1}{2}\ бассейна,\ \]

\[если\ \frac{5}{x} - заполнит\ первая\ \]

\[труба\ за\ 5\ ч,\]

\[затем\ \frac{9}{y} - вторая\ труба\ за\ 9\ ч.\]

\[Составляем\ систему\ \]

\[уравнений:\]

\[\left\{ \begin{matrix} \frac{12}{x} + \frac{12}{y} = 1\ \ \ \ | \cdot 3 \\ \frac{5}{x} + \frac{9}{y} = \frac{1}{2}\ \ \ \ \ \ | \cdot 4 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{36}{x} + \frac{36}{y} = 3 \\ \frac{20}{x} + \frac{36}{y} = 2\ \\ \end{matrix} - \right.\ \]

\[\left\{ \begin{matrix} \frac{16}{x} = 1\ \ \ \ \ \ \ \ \ \\ \frac{36}{y} = 2 - \frac{20}{x} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x = 16\ \ \ \ \ \ \ \ \\ y = \frac{36 \cdot 16}{12} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x = 16 \\ y = 48 \\ \end{matrix} \right.\ \]

\[16\ ч - требуется\ первой\ \]

\[трубе,\ чтобы\ заполнить\ \]

\[бассейн;\]

\[48\ ч - требуется\ второй\ \]

\[трубе.\]

\[Ответ:16\ ч;48\ ч.\ \]

\[\boxed{\text{494.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

\[Решение\ квадратных\ \]

\[неравенств.\]

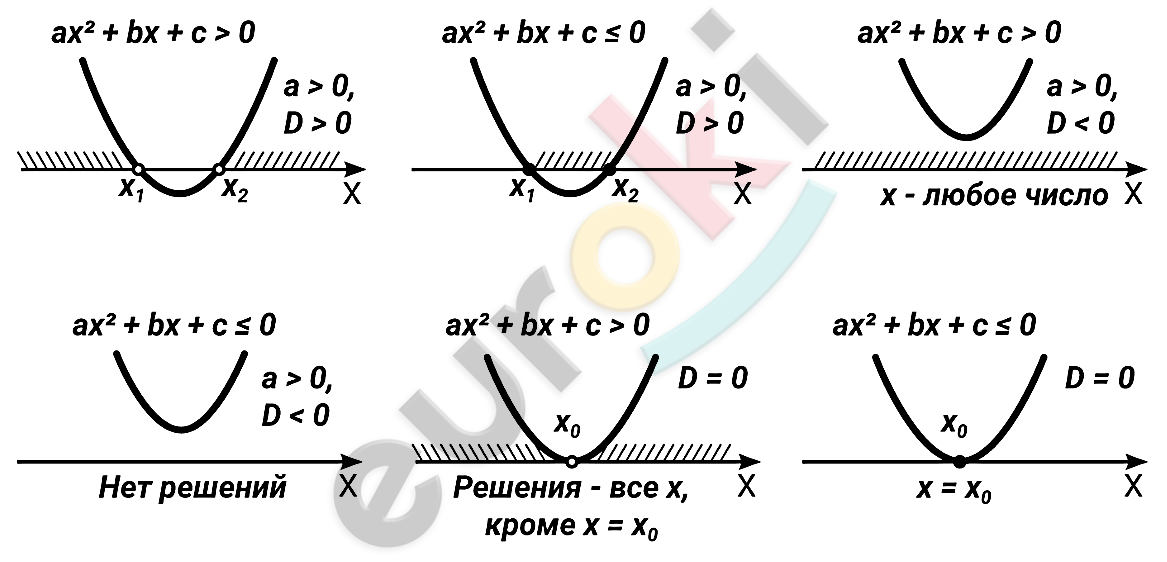
Решение.

\[1)\ x^{2} - 2x - 11 < \frac{1}{4}\ \ \ \ \ \ \ \ | \cdot 4\]

\[4x^{2} - 8x - 44 - 1 < 0\]

\[4x^{2} - 8x - 45 < 0\]

\[D = 64 + 720 = 784\]

\[x_{1,2} = \frac{8 \pm 28}{8}\]

\[x_{1} = - 2,5;\ \ \ x_{2} = 4,5\]

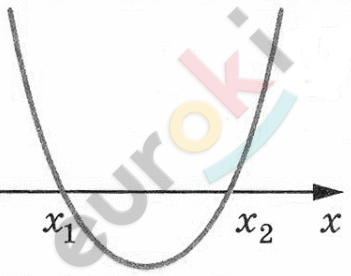
\[Ответ:\ x \in \ ( - 2,5;4,5).\]

\[2) - 3x^{2} + 8x + 6 \geq - \frac{2}{3}\ \ \ | \cdot 3\]

\[- 9x^{2} + 24x + 18 + 2 \geq 0\]

\[- 9x^{2} + 24x + 20 \geq 0\]

\[9x^{2} - 24x - 20 \leq 0\]

\[D = 576 + 720 = 1296\]

\[x_{1,2} = \frac{- 24 \pm 36}{- 18}\]

\[x_{1} = - \frac{2}{3};\ \ \ x_{2} = \frac{10}{3} = 3\frac{1}{3}\]

\[Ответ:x \in \left\lbrack - \frac{2}{3};\ 3\frac{1}{3} \right\rbrack\text{.\ }\]