Решебник по алгебре 9 класс Мерзляк Задание 490

 

\[\boxed{\text{490\ (490).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\frac{км}{ч} - скорость\ \]

\[скорого\ поезда,\ \]

\[а\ y\ \frac{км}{ч} - скорость\ \]

\[товарного\ поезда.\]

\[Тогда\ \frac{450}{x}\ ч - время\ пути\ \]

\[скорого\ поезда\ от\ M\ до\ N,\ \]

\[а\ \frac{450}{y}\ ч - время\]

\[пути\ товарного\ поезда\ от\ M\ до\ \]

\[N.\ Значит,\ 3x\ км -\]

\[проехал\ первый\ \]

\[поезд\ до\ отъезда\ товарного.\ \]

\[По\ условию\ известно,\]

\[\ что\ скорый\ поезд\ \]

\[преодолевает\ расстояние\ на\ \]

\[7\ ч\ 30\ мин\ быстрее.\]

\[Составляем\ систему\ \]

\[уравнений:\]

\[\left\{ \begin{matrix} 3x + 3(x + y) = 450\ \ \ \ \ \\ \frac{450}{y} - \frac{450}{x} = 7,5\ \ \ \ | \cdot \frac{1}{15} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 6x + 3y = 450\ \ \ \ |\ :3 \\ \frac{30}{y} - \frac{30}{x} = \frac{1}{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 2x + y = 150\ \\ \frac{30(x - y)}{\text{xy}} = \frac{1}{2} \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 2x + y = 150\ \ \ \ \\ 60(x - y) = xy \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} y = 150 - 2x\ \ \ \\ 60(x - y) = xy \\ \end{matrix} \right.\ \]

\[60 \cdot (x - 150 + 2x) =\]

\[= x \cdot (150 - 2x)\]

\[60x - 9000 + 120x -\]

\[- 150x + 2x^{2} = 0\]

\[2x^{2} + 30x - 9000 = 0\ \ \ |\ :2\]

\[x^{2} + 15x - 4500 = 0\]

\[D = 225 + 18000 = 18225\]

\[x_{1} = \frac{- 15 - 135}{2} = - 75 -\]

\[не\ удовлетворяет.\]

\[x_{2} = \frac{- 15 + 135}{2} = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ скорого\ поезда.\]

\[150 - 2 \cdot 60 = 30\ \left( \frac{км}{ч} \right) -\]

\[скорость\ товарного\ поезда.\]

\[Ответ:30\frac{км}{ч};60\frac{км}{ч}\text{.\ \ }\]

\[\boxed{\text{490.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

\[Решение\ квадратных\ \]

\[неравенств.\]

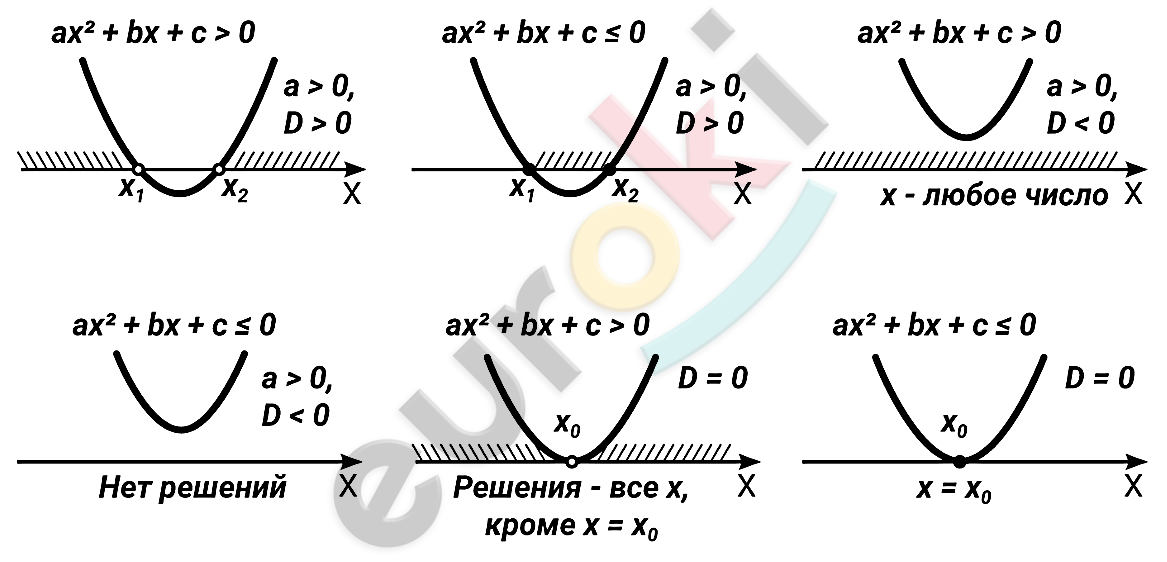
Решение.

\[1)\text{\ x}^{2} > 1\]

\[x^{2} - 1 > 0\]

\[(x - 1)(x + 1) > 0\]

\[x = - 1;\ \ x = 1.\]

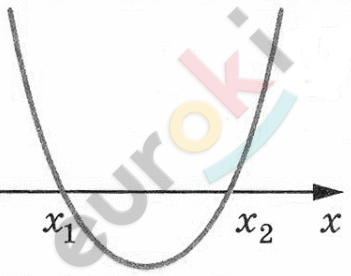
\[Ответ:x \in ( - \infty;\ - 1) \cup (1;\ + \infty).\]

\[2)\ x^{2} < 3\]

\[x^{2} - 3 < 0\]

\[\left( x + \sqrt{3} \right)\left( x - \sqrt{3} \right) < 0\]

\[x = - \sqrt{3};\ \ x = \sqrt{3}.\]

\[Ответ:x \in \left( - \sqrt{3}; + \sqrt{3} \right).\]

\[3) - 3x^{2} \geq - 12x\]

\[- 3x^{2} + 12x \geq 0\]

\[- 3x(x - 4) \geq 0\]

\[3x(x - 4) \leq 0\]

\[x = 0;\ \ x = 4.\]

\[Ответ:x \in \lbrack 0;4\rbrack.\]

\[4) - 2x^{2} < - 128\]

\[x^{2} > 64\]

\[x^{2} - 64 > 0\]

\[(x - 8)(x + 8) > 0\]

\[x = - 8;\ \ x = 8.\]

\[Ответ:x \in ( - \infty; - 8) \cup (8;\ + \infty).\]