Решебник по алгебре 9 класс Мерзляк Задание 472
Задание 472



\[\boxed{\text{472\ (472).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\left\{ \begin{matrix} y = |x|\text{\ \ \ \ \ \ \ } \\ x^{2} + y = a \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\left\{ \begin{matrix} y = |x|\text{\ \ \ \ \ \ \ \ \ } \\ x^{2} + |x| = a \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x^{2} + x = a \\ y = x \\ x \geq 0 \\ \end{matrix} \right.\ \ \ \ \ \ и\ \ \ \ \ \left\{ \begin{matrix} x^{2} - x = a \\ y = - x \\ x < 0 \\ \end{matrix} \right.\ \]
\[Если\ a > 0,\ то\ 2\ решения,\ \]
\[так\ как\ в\ каждой\ системе\ \]
\[будет\ решение,\]
\[удовлетворяющее\ условию.\]
\[Если\ a = 0,\ то\ \left\{ \begin{matrix} x^{2} + x = 0 \\ x^{2} - x = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]
\[\left\{ \begin{matrix} x(x + 1) = 0 \\ x(x - 1) = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ }\left\{ \begin{matrix} x = 0 \\ x = 0 \\ \end{matrix} \right.\ \ \ и\ \]
\[\left\{ \begin{matrix} x = - 1(не\ удовл.) \\ x = 1\ \ \ (не\ удовл.) \\ \end{matrix} \right.\ \]
\[одно\ решение.\]
\[Если\ a < 0,\ то\ \left\{ \begin{matrix} x^{2} + x < 0 \\ x \geq 0 \\ \end{matrix} \right.\ -\]
\[неверно,\ нет\ решений.\]
\[Ответ:a > 0 - 2\ решения;\ \]
\[a = 0 - 1\ решение;a < 0 -\]
\[нет\ решений.\]
\[2)\ \left\{ \begin{matrix} x^{2} + y^{2} = a^{2} \\ |x| = 4\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ x = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 16 + y^{2} = a^{2} \\ \end{matrix} \right.\ \text{\ \ \ \ }\left\{ \begin{matrix} x < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ x = - 4\ \ \ \ \ \ \ \ \ \\ 16 + y^{2} = a^{2} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \\ y^{2} = a^{2} - 16 \\ \end{matrix} \right.\ \ \ \ \ и\ \ \ \ \ \]
\[\left\{ \begin{matrix} x < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ x = - 4\ \ \ \ \ \ \ \ \ \ \\ y^{2} = a^{2} - 16 \\ \end{matrix} \right.\ \]
\[Если - 4 < a < 4 - нет\ \]
\[решений,\ так\ как\ y^{2} > 0.\]
\[Если\ a < - 4\ или\ a > 4,\ система\ \]
\[имеет\ 4\ решения,\ так\ как\ в\ \]
\[каждой\ \]
\[системе\ будет\ по\ 2\ решения,\]
\[\ удовлетворяющих\ условию.\]
\[Если\ a = - 4\ \ или\ a = 4,\ \]
\[то\ 2\ решения:\]
\[\left\{ \begin{matrix} x = 4 \\ y = 0 \\ \end{matrix} \right.\ \ \ и\ \ \left\{ \begin{matrix} x = - 4 \\ y = 0 \\ \end{matrix} \right.\ \]
\[Ответ:если - 4 < a < 4,\ \]
\[то\ нет\ решений;\]
\[если\ a < - 4\ или\ a > 4,\ \]
\[то\ 4\ решения;\]
\[если\ a = - 4\ или\ a = 4,\ \]
\[то\ 2\ решения.\]
\[3)\ \left\{ \begin{matrix} y - x = 1 \\ xy = a\ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]
\[\left\{ \begin{matrix} y = 1 + x\ \ \ \ \ \ \ \ \ \\ x^{2} + x - a = 0 \\ \end{matrix} \right.\ \]
\[x^{2} + x - a = 0\]
\[D = 1 + 4a\]
\[D = 0\]
\[1 + 4a = 0\]
\[a = - \frac{1}{4}\ \Longrightarrow одно\ решение.\]
\[D > 0\]
\[a > - \frac{1}{4} \Longrightarrow 2\ решения.\]
\[D < 0\]
\[a < - \frac{1}{4} \Longrightarrow нет\ решений.\]
\[Ответ:\ a = - \frac{1}{4}\ \Longrightarrow одно\ \]
\[решение;\ a > - \frac{1}{4} \Longrightarrow 2\ \]
\[решения;\ \]
\[a < - \frac{1}{4} \Longrightarrow нет\ решений\ \]
\[4)\ \left\{ \begin{matrix} x^{2} + y^{2} = 4 \\ y = x^{2} + a\ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x^{2} + {(x}^{2} + {a)}^{2} - 4 = 0 \\ y = x^{2} + a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x^{4} + (2x + 1)x^{2} + a^{2} - 4 = 0 \\ y = x^{2} + a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[Пусть\ x^{2} = t,\ \ тогда\]
\[t^{2} + (2a + 1) \cdot t + a^{2} - 4 = 0\]
\[D = 4a^{2} + 4a + 1 - 4a^{2} +\]
\[+ 16 = 17 + 4a\]
\[D = 0;\ a = - \frac{17}{4} \Longrightarrow 2\ решения.\]
\[- 2 < a < 2,\ \ \]
\[t^{2} + n \cdot t = 0 \Longrightarrow 2\ решения.\]
\[D < 0,\ \ \]
\[a < - \frac{17}{4} - нет\ решений.\]
\[Если - \frac{17}{4} < a < - 2,\]
\[то\ 4\ решения,\ \]
\[по\ \ 2\ решения\ в\ системах\]
\[\ \left\{ \begin{matrix} x^{2} = t\ \ \ \ \ \ \ \ \\ y = x^{2} + a \\ \end{matrix} \right.\ .\]
\[Если\ a = - 2,\ \]
\[то\ (y + 2)(y - 1) = 0,\ y =\]
\[= - 2\ \ или\ y = 1,\ при\ этом\]
\[x^{2} = 0\ \ или\ x^{2} = 3 \Longrightarrow 3\ \]
\[решения.\]
\[Если\ a = 2,\ то\ 1\ решение,\ \]
\[так\ как\ \]
\[(y - 2)(y + 3) = 0,\ y = 2\ или\ \]
\[y = - 3,\ \ \text{\ \ x}^{2}\ при\ этом\]
\[x^{2} = 0\ \ или\ \ x^{2} = - 5 \Longrightarrow\]
\[\Longrightarrow решение\ x = 0.\]

\[\boxed{\text{472.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
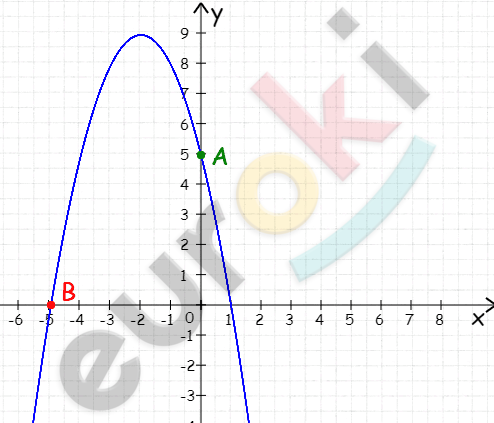
\[y = - x^{2} - 4x + 5\]
\[x_{0} = - 2,\ \ \]
\[y_{0} = - 4 + 8 + 5 = 9,\]
\[\text{\ \ }( - 2;9)\]
\[x_{1} = 0,\ \ y = 5,\ \ (0;5)\]
\[- x^{2} - 4x + 5 = 0\]
\[x_{1} + x_{2} = - 4,\ \ x_{1} = - 5,\]
\[\ \ ( - 5;0)\]
\[x_{1}x_{2} = - 5,\ \ x_{2} = 1,\ \ \]
\[(1;0)\]
 \(\text{\ \ }\)
\(\text{\ \ }\)
\[1)\ если\ a < 9,\ то\ уравнение\ \]
\[имеет\ 2\ корня.\ \]
\[2)\ если\ a = 9,\ то\ уравнение\]
\[\ имеет\ 1\ корень.\ \]
\[3)\ если\ a > 9,\ то\ уравнение\ \]
\[не\ имеет\ корней.\ \]




