Решебник по алгебре 9 класс Мерзляк Задание 205

 

\[\boxed{\text{205\ (205).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ |x - 2| \leq 3,6\]

\[- 3,6 \leq x - 2 \leq 3,6\]

\[- 1,6 \leq x \leq 5,6\]

\[Ответ:x \in \lbrack - 1,6;5,6\rbrack.\]

\[2)\ |2x + 3| < 5\]

\[- 5 < 2x + 3 < 5\]

\[- 8 < 2x < 2\]

\[- 4 < x < 1\]

\[Ответ:x \in ( - 4;1).\]

\[3)\ |x + 3| > 9\]

\[x + 3 > 9\ \ \ или\ \ \ x + 3 < - 9\]

\[\ \ \ \ \ \ \ \ x > 6\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x < - 12\]

\[Ответ:x \in ( - \infty;\ - 12) \cup (6; + \infty).\]

\[4)\ |7 - 3x| \geq 1\]

\[7 - 3x \leq - 1\ \ \ или\ \ \ 7 - 3x \geq 1\]

\[\ \ \ \ \ - 3x \leq - 8\ \ \ \ \ \ \ \ \ \ \ \ - 3x \geq - 6\]

\[\ \ \ \ \ \ \ \ \ \ \ x \geq \frac{8}{3}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\ x \leq 2\]

\[Ответ:x \in ( - \infty;2\rbrack \cup \left\lbrack 2\frac{2}{3};\ + \infty \right).\]

\[5)\ |x + 3| + 2x \geq 6\]

\[|x + 3| \geq 6 - 2x\]

\[x + 3 \leq 2x - 6\ \ \ или\ \ \ \]

\[x + 3 \geq 6 - 2x\]

\[\ \ \ \ \ \ - x \leq - 9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3x \geq 3\]

\[\ \ \ \ \ \ \ \ \ \ x \geq 9\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }x \geq 1\]

\[Ответ:x \in \lbrack 1;\ + \infty).\]

\[6)\ |x - 4| - 6x < 15\]

\[|x - 4| < 15 + 6x\]

\[Ответ:x \in \left( - 1\frac{4}{7};\ + \infty \right)\text{.\ }\]

\[\boxed{\text{205.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\frac{км}{ч} -\]

\[первоначальная\ скорость\ \]

\[всадника,\ а\ скорость\]

\[на\ обратном\ пути\ (x + 3)\frac{км}{ч}\text{.\ }\]

\[Значит,\ из\ Вишневое\ \]

\[в\ Яблоневое\ всадник\ \]

\[проскакал\ за\ \frac{15}{x}\ ч,\ а\ обратно -\]

\[за\ \ \frac{15}{x + 3}\ ч.\]

\[По\ условию\ известно,\ что\ на\ \]

\[обратный\ путь\ всадник\ \]

\[затратил\ на\ \frac{15}{60}\ ч\ меньше.\]

\[Составляем\ уравнение:\]

\[\frac{15}{x} - \frac{15}{x + 3} - \frac{1}{4} = 0;\ \ \ \ \ \ \ \ x \neq 0;\ \ \ \ \ \]

\[x \neq - 3\]

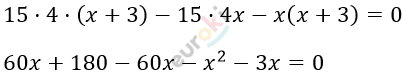
\[- x^{2} - 3x + 180 = 0\]

\[x^{2} + 3x - 180 = 0\]

\[D = 9 + 720 = 729\]

\[x = \frac{- 3 + 27}{2} = 12\ \left( \frac{км}{ч} \right) -\]

\[первоначальная\ скорость\ \]

\[всадника.\]

\[x = \frac{- 3 - 27}{2} = - 15 \Longrightarrow не\ \]

\[удовлетворяет\ условию.\]

\[Ответ:12\ \frac{км}{ч}.\]