Решебник по алгебре 9 класс Рурукин контрольные работы КР-2. Квадратичная функция. Степенная функция. Корень n-й степени Вариант 5

Условие:

1. Определите расстояние между осями симметрии графиков функции

y=-x²+2x+1 и y=2x²+12x+5.

2. Найдите область определения и область значений функции

y=4√(3x-6)+2x^2+4x-5.

3. Найдите наибольшее значение функции y=(3x^2-6x+23)/(x^2-2x+5). При каком значении x оно достигается?

4. Постройте график функции y=x²-5|x|+4.

5. Упростите выражение (x-15)/(√(x+1)-4)-(x-3)/(2+√(x+1)).

6. При каких значениях b и с точка A(-1;-10) является вершиной параболы y=2x²+bx+c?

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = - x^{2} + 2x + 1\ \ \]

\[и\ \ \]

\[y = 2x^{2} + 12x + 5\]

\[Уравнения\ осей\ симметрий\ \]

\[для\ \ данных\ парабол:\]

\[1)\ x_{0} = - \frac{b}{2a} = - \frac{2}{- 2} = 1;\]

\[2)\ x_{0} = - \frac{b}{2a} = - \frac{12}{4} = - 3.\]

\[Расстояние\ между\ этими\ \]

\[прямыми:\]

\[1 - ( - 3) = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = 4\sqrt{3x - 6} + 2x^{2} + 4x - 5\]

\[3x - 6 \geq 0\]

\[3x \geq 6\]

\[x \geq 2.\]

\[D(y) = \lbrack 2; + \infty).\]

\[Так\ как\ функции\ возрастают:\]

\[y(2) = 4 \cdot 0 + 2 \cdot 4 + 4 \cdot 2 - 5 = 11.\]

\[E(y) = \lbrack 11;\ + \infty).\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{3x^{2} - 6x + 23}{x^{2} - 2x + 5} =\]

\[= \frac{3x^{2} - 6x + 15 + 8}{x^{2} - 2x + 5} =\]

\[= \frac{3\left( x^{2} - 2x + 5 \right) + 8}{x^{2} - 2x + 5} =\]

\[= 3 + \frac{8}{(x - 1)^{2} + 4}\]

\[Наибольшее\ значение\ функция\ \]

\[достигает,\ если\ второе\ \ \]

\[слагаемое\ максимально,\ то\ \ \]

\[есть\ знаменатель\ дроби\ \]

\[минимальный.\]

\[Получаем,\ что\ при\ x = 1:\]

\[y = 3 + \frac{8}{4} = 5.\]

\[Ответ:y_{\max} = 5\ при\ x = 1.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

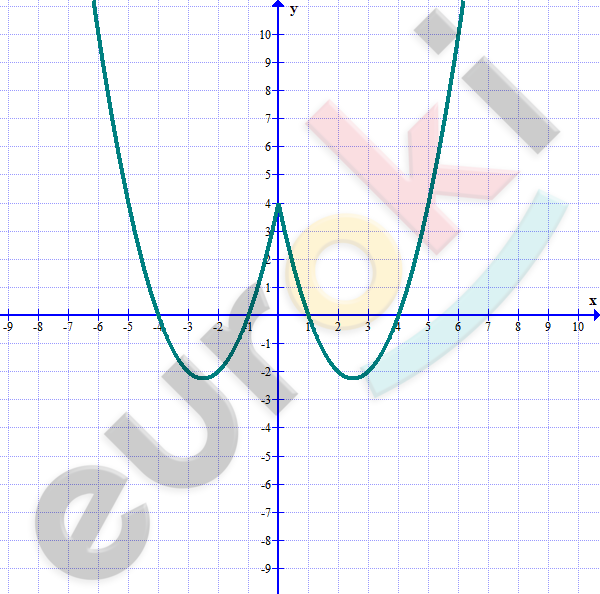
\[y = x^{2} - 5|x| + 4\]

\[x \geq 0:\]

\[y = x^{2} - 5x + 4\]

\[Вершина\ параболы:\ \]

\[(2,5;\ - 2,25).\]

\[Строим\ график\ и\ отображаем\ \]

\[его\ симметрично\ влево.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[\frac{x - 15}{\sqrt{x + 1} - 4} - \frac{x - 3}{2 + \sqrt{x + 1}}\]

\[y = \sqrt{x + 1};\ \ \]

\[y^{2} = x + 1;\ \ \ \]

\[x = y^{2} - 1.\]

\[\frac{y^{2} - 1 - 15}{y - 4} - \frac{y^{2} - 1 - 3}{2 + y} =\]

\[= \frac{y^{2} - 16}{y - 4} - \frac{y^{2} - 4}{y + 2} =\]

\[= \frac{(y - 4)(y + 4)}{y - 4} - \frac{(y - 2)(y + 2)}{y + 2} =\]

\[= y + 4 - y + 2 = 6.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[y = 2x^{2} + bx + c;\ \ \ A( - 1; - 10).\]

\[x = - \frac{b}{2a}:\]

\[- 1 = - \frac{b}{4}\]

\[- b = - 4\]

\[b = 4.\]

\[x = - 1:\]

\[- 10 = 2 \cdot 1 - 4 + c\]

\[c = - 10 + 2\]

\[c = - 8.\]

\[Ответ:b = 4;\ \ c = - 8.\]