Решебник по алгебре 9 класс Рурукин контрольные работы КР-2. Квадратичная функция. Степенная функция. Корень n-й степени Вариант 4

Условие:

1. Найдите область значения функции y=-3x²-6x+5, если x∈[-2;1].

2. Найдите область определения и область значений функции

y=2√(3x-6)+6x-5.

3. Вычислите наибольшее значение функции y=8/(x^2-4x+6)+1.

4. Вычислите 4∜(5 1/16)+6∛(-2 10/27).

5. Упростите выражение 3√x (1/(√x-4)+1/(√x+4))+96/(16-x).

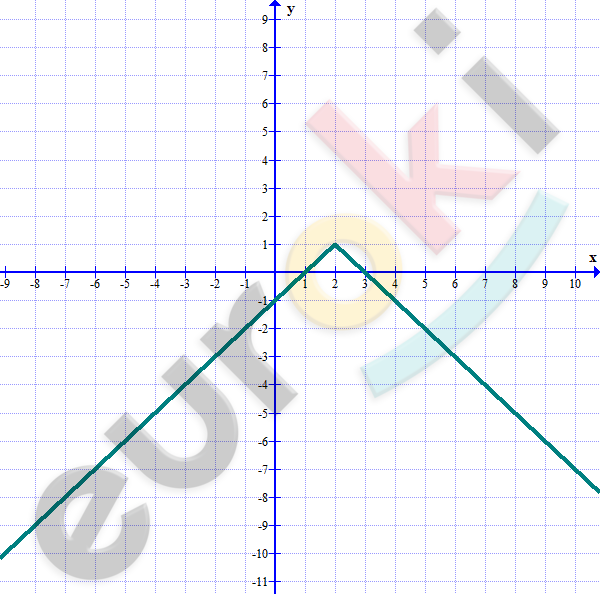
6. Постройте график функции y=-|x-2|+1.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = - 3x^{2} - 6x + 5;\ \ x \in \lbrack - 2;1\rbrack\]

\[y( - 2) = - 3 \cdot 4 + 12 + 5 = 5;\]

\[y( - 1) = - 3 \cdot 1 + 6 + 5 = 8;\]

\[y(1) = - 3 - 6 + 5 = - 4.\]

\[D(y) = \lbrack - 4;8\rbrack.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = 2\sqrt{3x - 6} + 6x - 5\]

\[a > 0 - ветви\ вверх.\]

\[3x - 6 \geq 0\]

\[3x \geq 6\]

\[x \geq 2\]

\[D(y) = \lbrack 2; + \infty).\]

\[y(2) = 2 \cdot \sqrt{3 \cdot 2 - 6} + 6 \cdot 2 - 5 = 7.\]

\[E(y) = \lbrack 7; + \infty).\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{8}{x^{2} - 4x + 6} + 1 =\]

\[= \frac{8}{\left( x^{2} - 4x + 4 \right) + 2} + 1 =\]

\[= \frac{8}{(x - 2)^{2} + 2} + 1\]

\[Наибольшее\ значение\ \ \]

\[функция\ достигает,\ если\ \]

\[первое\ слагаемое\ \ \]

\[максимально,\ то\ есть\ \]

\[знаменатель\ \ дроби\ \]

\[минимальный.\]

\[Получаем,\ что\ при\ x = 2:\ \]

\[y = \frac{8}{(2 - 2)^{2} + 2} + 1 =\]

\[= 4 + 1 = 5.\]

\[Ответ:y_{\max} = 5\ при\ x = 2.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[4\sqrt[4]{5\frac{1}{16}} + 6\sqrt[3]{- 2\frac{10}{27}} =\]

\[= 4\sqrt[4]{\frac{81}{16}} + 6\sqrt[3]{- \frac{64}{27}} =\]

\[= 4 \cdot \frac{3}{2} + 6 \cdot \left( - \frac{4}{3} \right) =\]

\[= 6 - 8 = - 2.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[3\sqrt{x}\left( \frac{1^{\text{√}x + 4\ }}{\sqrt{x} - 4} + \frac{1^{\text{√}x - 4}}{\sqrt{x} + 4} \right) + \frac{96}{16 - x} =\]

\[= 3\sqrt{x} \cdot \frac{\sqrt{x} + 4 + \sqrt{x} - 4}{x - 16} - \frac{96}{x - 16} =\]

\[= \frac{3\sqrt{x} \cdot 2\sqrt{x} - 96}{x - 16} = \frac{6x - 96}{x - 16} =\]

\[= \frac{6 \cdot (x - 16)}{x - 16} = 6.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[y = - |x - 2| + 1\]

\[Сдвинем\ график\ функции\ \ \]

\[y = - |x|\ на\ 2\ ед.\ вправо\ и\ \]

\[на\ 1\ ед.\ вверх.\]