Решебник по алгебре 9 класс Рурукин контрольные работы КР-1. Функция. Квадратный трехчлен Вариант 4

Условие:

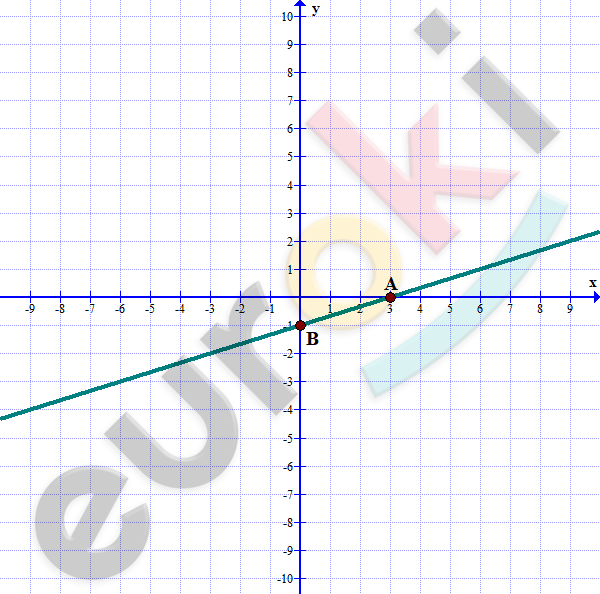
1. График линейной функции проходит через точки A(3; 0) и B(0;-1). Постройте график и задайте функцию формулой.

2. Дана функция y=(x-3)/(1-2x). Найдите зависимость величины x от переменной y.

3. Найдите наибольшее значение квадратного трехчлена 2x^2+12x+3.

4. Сократите дробь (9x^2-6x-8)/(6x^2-5x-4).

5. Найдите область определения и область значений функции y=2√(4-|x|)-1.

6. Найдите наибольшую возможную площадь прямоугольника, если его периметр равен 80 см.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = kx + b\]

\[A(3;0);\ \ B(0; - 1).\]

\[- 1 = 0x + b\]

\[b = - 1.\]

\[0 = 3k - 1\]

\[3k = 1\]

\[k = \frac{1}{3}.\]

\[Формула\ функции:\]

\[y = \frac{1}{3}x - 1.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{x - 3}{1 - 2x}\]

\[(1 - 2x)y = x - 3\]

\[y - 2xy = x - 3\]

\[y + 3 = x + 2xy\]

\[y + 3 = x(1 + 2y)\]

\[x = \frac{y + 3}{2y + 1}.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[2x^{2} + 12x + 3 =\]

\[= 2 \cdot \left( x^{2} + 6x + 7 \right) =\]

\[= 2 \cdot \left( x^{2} + 6x + 9 - 2 \right) =\]

\[= 2 \cdot {((x + 3)}^{2} - 2) =\]

\[= 2 \cdot {(x + 3)}^{2} - 4\ \]

\[Наименьшее\ значение\ ( - 4)\ \]

\[при\ x = - 3.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{9x^{2} - 6x - 8}{6x^{2} - 5x - 4}\]

\[1)\ 9x^{2} - 6x - 8 =\]

\[= 9 \cdot \left( x - \frac{4}{3} \right)\left( x + \frac{2}{3} \right) =\]

\[= (3x - 4)(3x + 2)\]

\[D = 9 + 72 = 81\]

\[x_{1} = \frac{3 + 9}{9} = \frac{12}{9} = \frac{4}{3};\]

\[x_{2} = \frac{3 - 9}{9} = - \frac{6}{9} = - \frac{2}{3}.\]

\[2)\ 6x^{2} - 5x - 4 =\]

\[= 6 \cdot \left( x - \frac{4}{3} \right)\left( x + \frac{1}{2} \right) =\]

\[= (3x - 4)(2x + 1)\]

\[D = 25 + 96 = 121\]

\[x_{1} = \frac{5 + 11}{12} = \frac{16}{12} = \frac{4}{3};\]

\[x_{2} = \frac{5 - 11}{12} = - \frac{6}{12} = - \frac{1}{2}.\]

\[\frac{9x^{2} - 6x - 8}{6x^{2} - 5x - 4} =\]

\[= \frac{(3x - 4)(3x + 2)}{(3x - 4)(2x + 1)} =\]

\[= \frac{3x + 2}{2x + 1}\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[y = 2\sqrt{4 - |x|} - 1\]

\[4 - |x| \geq 0\]

\[|x| = 4\]

\[x = \pm 4\]

\[- 4 \leq x \leq 4\]

\[D(y) = \lbrack - 4;4\rbrack.\]

\[x = \pm 4 \rightarrow y = - 1.\]

\[x = 0 \rightarrow y = 3.\]

\[E(y) = y \in \lbrack - 1;3\rbrack.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[Максимальная\ площадь\ у\ \]

\[прямоугольника\ в\ том\ случае,\ \]

\[если\ этот\ прямоугольник -\]

\[квадрат.\]

\[То\ есть,\ P = 4a = 80.\]

\[4a = 80\]

\[a = 20\ (см) - сторона\ \]

\[прямоугольника.\]

\[S = a^{2} = 20^{2} = 400\ см^{2}.\]

\[Ответ:\ 400\ см^{2}.\ \]