Решебник по алгебре 9 класс Рурукин контрольные работы КР-1. Функция. Квадратный трехчлен Вариант 2

Условие:

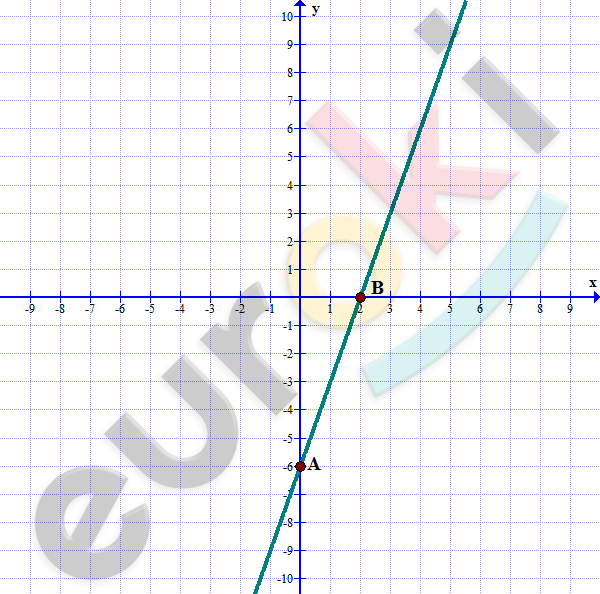
1. Найдите координаты точек пересечения графика функции y=3x-6 с осями координат. Постройте график этой функции.

2. При каком значении аргумента значение функции y=(-2x-1)/(x+2) равно -5?

3. Разложите на множители квадратный трехчлен 3x^2-5x-2.

4. Сократите дробь (x^2-x-2)/(2-x).

5. Найдите область определения и область значений функции y=√(x+1)+2.

6. Найдите наибольшее значение квадратного трехчлена -x^2-6x+3.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = 3x - 6\]

\[x = 0:\]

\[y = 3 \cdot 0 - 6 = - 6.\]

\[y = 0:\]

\[3x - 6 = 0\]

\[3x = 6\]

\[x = 2.\]

\[Точки\ пересечения:\]

\[A(0; - 6);B(2;0).\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{- 2x - 1}{x + 2};\ \ y = - 5\]

\[\frac{- 2x - 1}{x + 2} = - 5^{\backslash x + 2}\]

\[\frac{- 2x - 1 + 5x + 10}{x + 2} = 0\]

\[\frac{3x + 9}{x + 2} = 0;\ \ \ x \neq - 2\]

\[3x + 9 = 0\]

\[3x = - 9\]

\[x = - 3\]

\[Ответ:при\ x = - 3.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[3x^{2} - 5x - 2 =\]

\[= 3 \cdot (x - 2)\left( x + \frac{1}{3} \right) =\]

\[= (x - 2)(3x + 1)\]

\[D = 25 + 24 = 49\]

\[x_{1} = \frac{5 + 7}{6} = 2;\ \ \]

\[x_{2} = \frac{5 - 7}{6} = - \frac{2}{6} = - \frac{1}{3}.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{x^{2} - x - 2}{2 - x} = \frac{(x - 2)(x + 1)}{- (x - 2)} =\]

\[= - (x + 1) = - x - 1\]

\[x^{2} - 2x + x - 2 =\]

\[= x(x - 2) + (x - 2) =\]

\[= (x - 2)(x + 1).\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[y = \sqrt{x + 1} + 2\]

\[x + 1 \geq 0\]

\[x \geq - 1.\]

\[D(y) = x \in \lbrack - 1; + \infty).\]

\[y \geq 2\]

\[E(y) = y \in \lbrack 2; + \infty).\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[- x^{2} - 6x + 3 =\]

\[= - \left( x^{2} - 6x + 9 \right) + 12 =\]

\[= - (x - 3)^{2} + 12\]

\[Наибольшее\ значение\ \]

\[равно\ 12\ при\ x = 3.\]

\[Ответ:12.\]