Решебник по алгебре 9 класс Рурукин контрольные работы КР-2. Квадратичная функция. Степенная функция. Корень n-й степени Вариант 2

Условие:

1. Постройте график функции y=x²+8x+5. Укажите координаты вершины параболы.

2. Найдите область значения функции y=-x²+6x+2.

3. Определите координаты точек пересечения параболы y=1/5*x² и прямой y=20-3x.

4. Найдите a и постройте график функции y=x²+ax-3, если известно, что он проходит через точку (-2; 5).

5. Вычислите 12∛(-1/27)+15∜(3 13/81).

6. Постройте график функции y=|x-1|+1.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

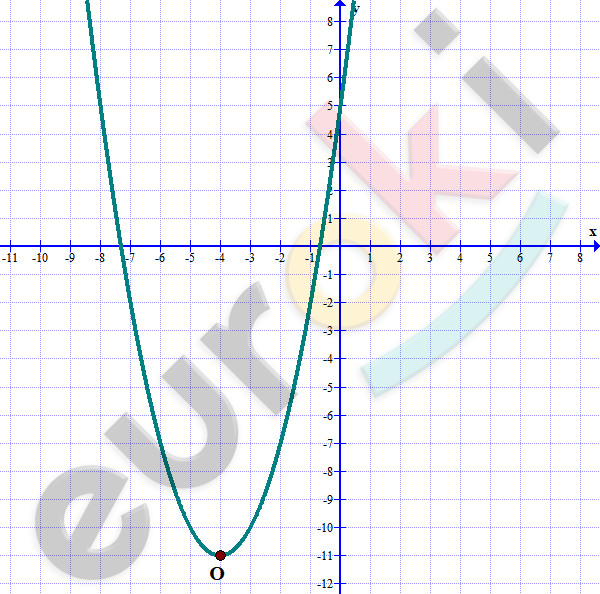
\[y = x^{2} + 8x + 5\]

\[a > 0 - ветви\ вверх.\]

\[x_{0} = - \frac{b}{2a} = - \frac{8}{2} = - 4;\]

\[y_{0} = 16 - 32 + 5 = - 11.\]

\[Вершина\ параболы\ в\ точке\ \]

\[O( - 4;\ - 11).\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = - x^{2} + 6x + 2\]

\[a < 0 - ветви\ вниз.\]

\[x_{0} = - \frac{b}{2a} = \frac{6}{2} = 3;\]

\[y_{0} = - 9 + 18 + 2 = 11.\]

\[D(y) = ( - \infty;11\rbrack.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{1}{5}x^{2}\ и\ y = 20 - 3x\]

\[\frac{1}{5}x^{2} = 20 - 3x\]

\[\frac{1}{5}x^{2} + 3x - 20 = 0\ \ \ \ \ \ | \cdot 5\]

\[x^{2} + 15x - 100 = 0\]

\[x_{1} + x_{2} = - 15;\ \ \ \ x_{1} \cdot x_{2} = - 100\]

\[x_{1} = - 20;\ \ \ x_{2} = 5.\]

\[y_{1} = \frac{1}{5} \cdot 400 = 80;\]

\[y_{2} = \frac{1}{5} \cdot 25 = 5.\]

\[Точки\ пересечения\ графиков:\]

\[( - 20;80);\ \ (5;5).\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[y = x^{2} + ax - 3;\ \ \ \ ( - 2;5)\]

\[5 = ( - 2)^{2} - 2a - 3\]

\[4 - 2a - 3 = 5\]

\[- 2a = 5 - 1\]

\[- 2a = 4\]

\[a = - 2.\]

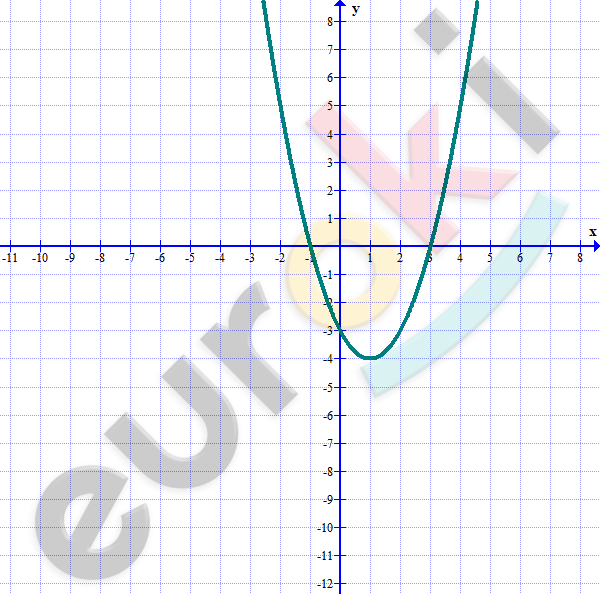
\[Искомый\ график\ функции:\]

\[y = x^{2} - 2x - 3\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[12\sqrt[3]{- \frac{1}{27}} + 15\sqrt[4]{3\frac{13}{81}} =\]

\[= 12 \cdot \left( - \frac{1}{3} \right) + 15\sqrt[4]{\frac{256}{81}} =\]

\[= - 4 + 15 \cdot \frac{4}{3} = - 4 + 20 = 16.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

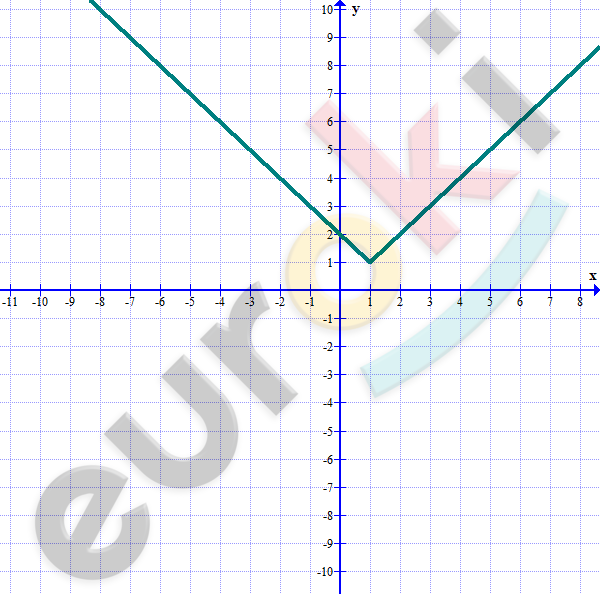
\[y = |x - 1| + 1\]

\[Сдвинем\ график\ y = |x|\ на\ \]

\[1\ ед.\ вправо\ и\ на\ 1\ ед.вверх.\]