Решебник по алгебре 8 класс Мерзляк ФГОС Задание 838

 

\[\boxed{\mathbf{838\ (838).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Расположим\ кусочки\ в\ порядке\ \]

\[увеличения\ массы:\]

\[m < m_{2} < \ldots < m_{9}.\]

\[В\ одну\ тарелку\ положили\ \]

\[m_{1},\ m_{3},\ m_{5},\ m_{7},\ \]

\[а\ в\ другую - m_{2},\ m_{4},\ m_{6},\ m_{8}.\]

\[а\ если\ в\ первую\ тарелку\ \]

\[положить\ m_{9},\ то\ \]

\[Следовательно,\ можно\ \]

\[разрезать\ m_{9}.\]

\[Ответ:можно.\]

\[\boxed{\mathbf{838.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[катера,\ тогда\ (x + 1)\frac{км}{ч} -\]

\[скорость\ по\ течению\ реки,\ \]

\[а\ (x - 1)\ \frac{км}{ч} - скорость\ \]

\[против\ течения.\]

\[По\ течению\ реки\ катер\ \]

\[затратил\ \frac{16}{x + 1}\ ч,\ а\ против\ \]

\[течения - \frac{30}{x - 1}\ ч.\]

\[По\ условию\ известно,\ что\ все\ \]

\[время\ пути\ 1,5\ ч.\]

\[Составляем\ уравнение:\]

\[\frac{16}{x + 1} + \frac{30}{x - 1} - 1,5 = 0;\ \ \ \ \]

\[x \neq - 1;\ \ \ x \neq 1\]

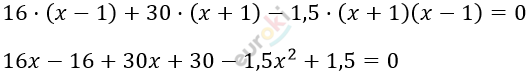
\[- 1,5x^{2} + 46x + 15,5 = 0\]

\[D = 2116 + 93 = 2209\]

\[x = \frac{- 46 - 47}{- 3} = 31\ \left( \frac{км}{ч} \right) -\]

\[скорость\ катера.\]

\[x = \frac{- 46 + 47}{- 3} = - \frac{1}{3} \Longrightarrow не\ \]

\[удовлетворяет\ условию.\]

\[Ответ:31\ \frac{км}{ч}.\]