Решебник по алгебре 8 класс Мерзляк ФГОС Задание 836

 

\[\boxed{\mathbf{836\ (836).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[\sqrt{\left( \sqrt{3} - 2 \right)^{2}} = \left| \sqrt{3} - 2 \right| =\]

\[= \left| \sqrt{3} - \sqrt{4} \right| = 2 - \sqrt{3},\ так\ как\]

\[\sqrt{3} - \sqrt{4} < 0\]

\[\boxed{\mathbf{836.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ м^{3}воды\ перекачивает\ \]

\[первый\ насос,\ а\ второй\ \]

\[(x - 5)м^{3}.\ Тогда\ первый\ \]

\[перекачивает\ \frac{90}{x}\ ч,\ \]

\[а\ второй - \frac{100}{x - 5}\ ч.\ \]

\[По\ условию\ известно,\ \]

\[то\ первый\ перекачивает\ \]

\[на\ 1\ час\ быстрее,и\ на\ 5\ м^{3}\]

\[больше,\ чем\ второй\ насос.\]

\[Составим\ уравнение:\ \]

\[\frac{90}{x} - \frac{100}{x - 5} + 1 = 0;\ \ \ \ \ \ x \neq 0;\ \ \ \]

\[x \neq 5\]

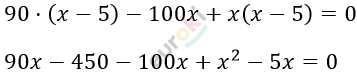
\[x^{2} - 15x - 450 = 0\]

\[D = 225 + 1800 = 2025\]

\[x = \frac{15 + 45}{2} = 30\ \left( м^{3} \right) -\]

\[перекачивает\ первый\ насос.\]

\[x = \frac{15 - 45}{2} = - 15 \Longrightarrow не\ \]

\[удовлетворяет\ условию.\]

\[30 - 5 = 25\ \left( м^{3} \right) -\]

\[перекачивает\ второй\ насос.\]

\[Ответ:25м³,\ 30\ м³\]