Решебник по алгебре 8 класс Мерзляк ФГОС Задание 834

 

\[\boxed{\mathbf{834\ (834).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[y = - 2x + 4\]

\[1)\ нуль\ функции:x = 2;\]

\[2)\ y > 0\ при\ x \in ( - \infty;2);\]

\[3)\ \text{M\ }( - 36;68):\ \]

\[68 = - 2 \cdot ( - 36) + 4\]

\[68 \neq 76\]

\[график\ не\ проходит\ через\ \]

\[( \cdot )M.\]

\[\boxed{\mathbf{834.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[автомобиля,\ а\ скорость\ \]

\[автобуса\ (x - 20)\ \frac{км}{ч}.Тогда\ \]

\[автомобиль\ проезжает\ \]

\[расстояние\ за\ \frac{240}{x}\ ч,\ \]

\[а\ автобус - за\ \ \frac{240}{x - 20}\ ч.\]

\[По\ условию\ известно,\ \]

\[что\ автобус\ приехал\ на\ 1\ час\ \]

\[позже.\]

\[Составляем\ уравнение:\]

\[\frac{240}{x} - \frac{240}{x - 20} + 1 = 0;\ \ \ \ \ \ x \neq 0;\ \ \ \ \]

\[x \neq 20\]

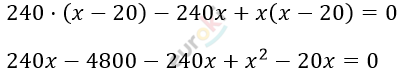
\[x^{2} - 20x - 4800 = 0\]

\[D = 400 + 19\ 200 = 19\ 600\]

\[x = \frac{20 + 140}{2} = 80\ \left( \frac{км}{ч} \right) -\]

\[скорость\ автомобиля.\]

\[x = \frac{20 - 140}{2} = - 60 \Longrightarrow не\ \]

\[удовлетворяет\ условию.\]

\[80 - 20 = 60\ \left( \frac{км}{ч} \right) -\]

\[скорость\ автобуса.\]

\[Ответ:80\ \frac{км}{ч};60\ \frac{км}{ч}.\]