Решебник по алгебре 8 класс Мерзляк ФГОС Задание 801

 

\[\boxed{\mathbf{801\ (801).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Записано\ число\ 1,\ следующее\ \]

\[число\ будет\ 2,\ затем\ 4;8;16;23;\]

\[28\ и\ т.д.\]

\[Наше\ число\ 123456789\ :9,\ \]

\[а\ числа,\ которые\ будет\ \]

\[записывать\ компьютер,\ \]

\[на\ 9\ делиться\ не\ будут.\ \]

\[Следовательно,\ 123456789\ на\ \]

\[экране\ не\ появится.\]

\[\boxed{\mathbf{80}\mathbf{1}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\ y = \frac{x² - 2x - 8}{x - 4}\]

\[x^{2} - 2x - 8 = 0\]

\[x_{1} + x_{2} = 2,\ \ x_{1} = 4\]

\[x_{1} \cdot x_{2} = - 8,\ \ x_{2} = - 2\]

\[y = \frac{x^{2} - 2x - 8}{x - 4} =\]

\[= \frac{(x - 4)(x + 2)}{(x - 4)} = x + 2\]

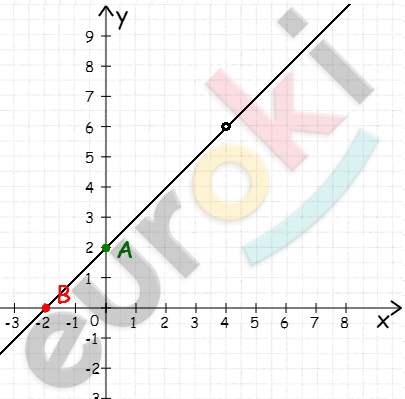
\[y = x + 2,\ \ x \neq 4\]

\[2)\ y = \frac{x^{2} - x - 2}{x + 1} - \frac{x^{2} - x - 30}{x + 5}\]

\[x² - x - 2 = 0\]

\[x_{1} + x_{2} = 1,\ \ x_{1} = 2\]

\[x_{1} \cdot x_{2} = - 2,\ \ x_{2} = - 1\]

\[\frac{x^{2} - x - 2}{x + 1} = \frac{(x - 2)(x + 1)}{(x + 1)} =\]

\[= x - 2\]

\[x^{2} - x - 30 = 0\]

\[x_{1} + x_{2} = - 1,\ \ x_{1} = 6\]

\[x_{1} \cdot x_{2} = - 30,\ \ x_{2} = - 5\]

\[\frac{x^{2} - x - 30}{x + 5} = \frac{(x - 6)(x + 5)}{(x + 5)} =\]

\[= x - 6\]

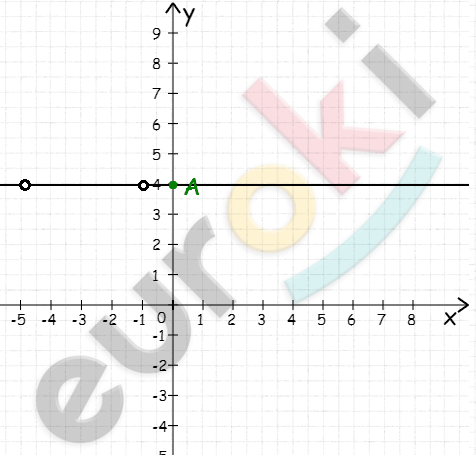
\[y = x - 2 - x + 6\]

\[y = 4,\ \ x \neq - 1,\ \ x \neq - 5\]