Решебник по алгебре 8 класс Мерзляк ФГОС Задание 716

 

\[\boxed{\mathbf{716\ (716).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[x_{1} = 7\]

\[x_{2} = ?\]

\[x² + px - 42 = 0\]

\[x_{1} \cdot x_{2} = - 42\]

\[x_{2} = - \frac{42}{x_{1}} = - \frac{42}{7} = - 6\]

\[x_{1} + x_{2} = - p\]

\[7 - 6 = 1 \Longrightarrow \ \ p = - 1\]

\[Ответ:x_{2} = - 6;\ \ p = - 1.\]

\[\boxed{\mathbf{71}\mathbf{6}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ \text{y\ }см - одна\ сторона\ \]

\[прямоугольника,\ тогда\ другая\ \]

\[сторона\ равна\ (y + 31)\ см.\ \]

\[По\ условию\ известно,\ \]

\[что\ диагональ\ равна\ 41\ см.\]

\[Используя\ теорему\ Пифагора,\ \]

\[составим\ уравнение:\]

\[(31 + y)^{2} + y^{2} = 41²\]

\[961 + 62y + y^{2} + y^{2} - 1681 =\]

\[= 0\]

\[2y^{2} + 62y - 720 = 0\]

\[y^{2} + 31y - 360 = 0\]

\[D = 961 + 4 \cdot 360 = 2401\]

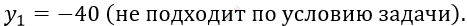
\[y_{2} = 9\ (см) - ширина\ \]

\[прямоугольника.\]

\[y + 31 = 9 + 31 = 40\ (см) -\]

\[длина\ прямоугольника.\]

\[Ответ:\ 9\ см\ и\ 40\ см.\]