Решебник по алгебре 8 класс Мерзляк ФГОС Задание 715

 

\[\boxed{\mathbf{715\ (715).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[x_{2} = ?\]

\[x² - 8x + q = 0\]

\[\left\{ \begin{matrix} x_{1} + x_{2} = 8 \\ x_{1} \cdot x_{2} = q \\ x_{1} = - 2\ \ \ \ \ \\ \end{matrix} \right.\ \]

\[x_{2} = 8 - x_{1}\]

\[x_{2} = 8 + 2 = 10\]

\[x_{1} \cdot x_{2} = - 2 \cdot 10 = - 20\]

\[q = - 20\]

\[Ответ:x_{2} = 10;\ \ q = - 20.\]

\[\boxed{\mathbf{71}\mathbf{5}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

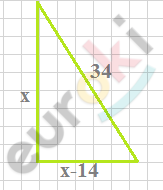
\[Пусть\ один\ катет\ равен\ \text{x\ }см,\ \]

\[тогда\ (x - 14)\ см - второй\ \]

\[катет.\]

\[По\ условию\ известно,\ что\ \]

\[гипотенуза\ равна\ 34\ см.\]

\[Составим\ уравнение\ \]

\[(теорема\ Пифагора):\]

\[x^{2} + (x - 14)^{2} = 34^{2}\]

\[x^{2} + x^{2} - 28x + 196 - 1156 =\]

\[= 0\]

\[2x² - 28x - 960 = 0\ \ \ |\ :2\]

\[x^{2} - 14x - 480 = 0\]

\[D = 196 + 4 \cdot 480 = 2116\]

\[x = \frac{14 \pm \sqrt{2116}}{2} = \frac{14 \pm 46}{2}\]

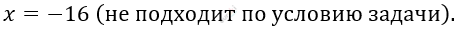
\[x = 30\ (см) - длина\ одного\ \]

\[катета.\]

\[x - 14 = 30 - 14 = 16\ (см) -\]

\[длина\ второго\ катета.\]

\[Ответ:16\ см\ и\ 30\ см.\]