Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Мерзляк ФГОС Вопросы к параграфу 15
Вопросы к параграфу 15
\[\ \boxed{\text{Вопросы}\text{\ }\text{к}\text{\ }\text{параграфу}\text{15.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\text{1.\ }}\]
\[Все\ натуральные\ числа,\ \]
\[противоположные\ им\ числа\ и\ \]
\[число\ нуль\ образуют\ \]
\[множество\ целых\ чисел.\ \]
\[\boxed{\text{2.\ }}\]
\[Множество\ целых\ чисел\ \]
\[обозначают\ буквой\ \text{Z.}\]
\[\boxed{\text{3.\ }}\]
\[Целые\ и\ дробные\ \]
\[числа\ образуют\ множество\ \]
\[рациональных\ чисел.\]
\[\boxed{\text{4.\ }}\]
\[Множество\ рациональных\ \]
\[чисел\ обозначают\ буквой\ \text{Q.}\]
\[\boxed{\text{5.\ }}\]
\[Каждое\ рациональное\ число\ \]
\[можно\ представить\ в\ виде\ \]
\[отношения\frac{m}{n};\ \ где\ m - целое\ \]
\[число,\ а\ n - натуральное\ \]
\[число.\]
\[\boxed{\text{6.\ }}\]
\[Каждое\ рациональное\ число\ \]
\[можно\ представить\ в\ виде\ \]
\[бесконечной\ периодической\ \]
\[дроби.\]
\[Каждая\ бесконечная\ \]
\[периодическая\ десятичная\ \]
\[дробь\ является\ записью\ \]
\[некоторого\ рационального\ \]
\[числа.\]
\[\boxed{\text{7.\ }}\]
\[Числа,\ не\ являющиеся\ \]
\[рациональными,\ называются\ \]
\[иррациональными.\]
\[\boxed{\text{8.\ }}\]
\[Множество\ действительных\ \]
\[чисел\ образует\ объединение\ \]
\[множеств\ иррациональных\ и\ \]
\[рациональных\ чисел.\]
\[\boxed{\text{9.\ }}\]
\[Множество\ действительных\ \]
\[чисел\ обозначают\ буквой\ \text{R.}\]
\[\boxed{\text{10.\ }}\]
\[Связь\ между\ множествами:\]
\[N \subset Z \subset Q \subset R.\]
\[\ \boxed{\text{Вопросы}\text{\ }\text{к}\text{\ }\text{параграфу}\text{15.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\text{1.\ }}\]
\[Все\ натуральные\ числа,\ \]
\[противоположные\ им\ числа\ и\ \]
\[число\ нуль\ образуют\ \]
\[множество\ целых\ чисел.\ \]
\[\boxed{\text{2.\ }}\]
\[Множество\ целых\ чисел\ \]
\[обозначают\ буквой\ \text{Z.}\]
\[\boxed{\text{3.\ }}\]
\[Целые\ и\ дробные\ \]
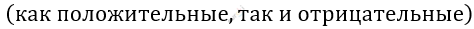
\[числа\ образуют\ множество\ \]
\[рациональных\ чисел.\]
\[\boxed{\text{4.\ }}\]
\[Множество\ рациональных\ \]
\[чисел\ обозначают\ буквой\ \text{Q.}\]
\[\boxed{\text{5.\ }}\]
\[Каждое\ рациональное\ число\ \]
\[можно\ представить\ в\ виде\ \]
\[отношения\frac{m}{n};\ \ где\ m - целое\ \]
\[число,\ а\ n - натуральное\ \]
\[число.\]
\[\boxed{\text{6.\ }}\]
\[Каждое\ рациональное\ число\ \]
\[можно\ представить\ в\ виде\ \]
\[бесконечной\ периодической\ \]
\[дроби.\]
\[Каждая\ бесконечная\ \]
\[периодическая\ десятичная\ \]
\[дробь\ является\ записью\ \]
\[некоторого\ рационального\ \]
\[числа.\]
\[\boxed{\text{7.\ }}\]
\[Числа,\ не\ являющиеся\ \]
\[рациональными,\ называются\ \]
\[иррациональными.\]
\[\boxed{\text{8.\ }}\]
\[Множество\ действительных\ \]
\[чисел\ образует\ объединение\ \]
\[множеств\ иррациональных\ и\ \]
\[рациональных\ чисел.\]
\[\boxed{\text{9.\ }}\]
\[Множество\ действительных\ \]
\[чисел\ обозначают\ буквой\ \text{R.}\]
\[\boxed{\text{10.\ }}\]
\[Связь\ между\ множествами:\]
\[N \subset Z \subset Q \subset R.\]
