Решебник по алгебре 8 класс Макарычев ФГОС Задание 986

 

\[\boxed{\text{986\ (986).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

аⁿ (а в n-ой степени) – число «n» называют показателем степени, а число «а» – основанием степени. Степень говорит нам о том, сколько раз следует умножить число «a» само на себя. Например, 3⁴=3*3*3*3=81.

При решении используем следующие правила:

1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание оставляют прежним:

\[\mathbf{a}^{\mathbf{m}}\mathbf{\bullet}\mathbf{a}^{\mathbf{n}}\mathbf{=}\mathbf{a}^{\mathbf{m + n}}\mathbf{.}\]

2. При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя, а основание оставляют прежним:

\[\mathbf{a}^{\mathbf{m}}\mathbf{\ :\ }\mathbf{a}^{\mathbf{n}}\mathbf{= \ }\mathbf{a}^{\mathbf{m - n}}\mathbf{.}\]

3. При возведении степени в степень (степень говорит нам о том, сколько раз следует умножить число само на себя. Например, 3⁴=3*3*3*3=81) показатели перемножаются, а основание остается прежним:

\[\mathbf{(}\mathbf{a}^{\mathbf{m}}\mathbf{)}^{\mathbf{n}}\mathbf{=}\mathbf{a}^{\mathbf{m \bullet n}}\mathbf{.}\]

4. Чтобы возвести дробь в отрицательную степень, нужно поменять местами числитель со знаменателем, а после возвести в степень уже без знака « – »:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{- n}}\mathbf{=}\left( \frac{\mathbf{b}}{\mathbf{a}} \right)^{\mathbf{n}}\mathbf{.}\]

5. Чтобы возвести дробь в степень, необходимо возвести в эту степень числитель и знаменатель:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{n}}\mathbf{=}\frac{\mathbf{a}^{\mathbf{n}}}{\mathbf{b}^{\mathbf{n}}}\mathbf{.}\]

6. Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй (перевернуть, поменяв местами числитель со знаменателем):

\[\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\ :\ }\frac{\mathbf{c}}{\mathbf{d}}\mathbf{=}\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\bullet}\frac{\mathbf{d}}{\mathbf{c}}\mathbf{=}\frac{\mathbf{a \bullet d}}{\mathbf{b \bullet c}}\mathbf{.}\]

7. Степень с отрицательным показателем – это дробь, числителем которой является единица, а знаменателем – данное число с положительным показателем:

\[\mathbf{a}^{\mathbf{- n}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{a}^{\mathbf{n}}}\mathbf{.}\]

Решение.

\[\textbf{а)}\ 5^{- 15} \cdot 5^{16} = 5^{- 15 + 16} = 5^{1} = 5\]

\[\textbf{б)}\ \left( \frac{1}{3} \right)^{- 4} \cdot \left( \frac{1}{3} \right)^{3} = 3^{4} \cdot \frac{1}{3^{3}} = 3^{1} =\]

\[= 3\]

\[\textbf{в)}\ 4^{- 8}\ :4^{- 9} = 4^{- 8 - (9)} = 4^{1} = 4\]

\[\textbf{г)}\ \left( \frac{1}{5} \right)²\ :\left( \frac{1}{5} \right)^{4} = \frac{1}{25}\ :\frac{1}{625} =\]

\[= \frac{1}{25} \cdot \frac{625}{1} = 25\]

\[\textbf{д)}\ \left( 2^{- 2} \right)^{- 3} = 2^{- 2 \cdot ( - 3)} = 2^{6} = 64\]

\[\textbf{е)}\ \left( {0,1}^{- 3} \right)^{- 1} = {0,1}^{- 3 \cdot ( - 1)} =\]

\[= 0,1³ = 0,001\]

\[\boxed{\text{986.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\textbf{а)}\ \left\{ \begin{matrix} 3 - 2a < 13 \\ 5a < 17\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix} - 2a < 10 \\ a < \frac{17}{5}\text{\ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\ \left\{ \begin{matrix} a > - 5 \\ a < 3,4 \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - 5;3,4)\]

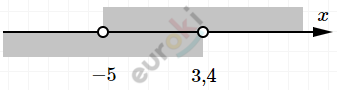
\[a = - 4;\ - 3;\ - 2;\ - 1;0;1;2;3.\]

\[\textbf{б)}\ \left\{ \begin{matrix} 12 - 6x \leq 0\ \ \ \ \ \ \ \ \\ 3x + 1 \leq 25 - x \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} - 6x \leq - 12\ \ \ \ \ \ \ \ \ \\ 3x + x \leq 25 - 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\left\{ \begin{matrix} x \geq 2\ \ \ \ \ \\ 4x \leq 24 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq 2 \\ x \leq 6 \\ \end{matrix} \right.\ \Longrightarrow \ \lbrack 2;6\rbrack\]

\[x = 2;3;4;5;6.\]

\[\textbf{в)}\ \left\{ \begin{matrix} 2 - 6y < 14 \\ 1 < 21 - 5y \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} - 6y < 12 \\ 5y < 20 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} y > - 2 \\ y < 4\ \ \ \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - 2;4)\]

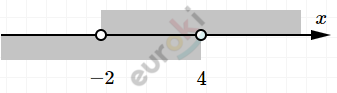
\[y = - 1;0;1;2;3.\]

\[\textbf{г)}\ \left\{ \begin{matrix} 3 - 4x < 15 \\ 1 - 2x > 0\ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\left\{ \begin{matrix} - 4x < 12 \\ - 2x > - 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} x > - 3 \\ x < 0,5 \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - 3;0,5)\]

\[x = - 2;\ - 1;0.\]