Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 820
Задание 820
\[\boxed{\text{820\ (820).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
| Неравенство, задающее числовой промежуток. | Обозначение и название числового промежутка. | Изображение числового промежутка на координатной прямой. |
|---|---|---|
| \[\mathbf{a \leq x \leq b}\] |
\[\left\lbrack \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[числовой\ отрезок\ \] |
 |
| \[\mathbf{a < x < b}\] |
\[\left( \mathbf{a;\ b} \right)\mathbf{- \ }\] \[\mathbf{интервал}\] |
 |
| \[\mathbf{a \leq x < b}\] |
\[\left\lbrack \mathbf{a;\ b} \right)\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{a < x \leq b}\] |
\[\left( \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{x \geq a}\] |
\[\left\lbrack \mathbf{a; + \infty} \right)\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
| \[\mathbf{x > a}\] |
\[\mathbf{(a; + \infty) -}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
| \[\mathbf{x \leq b}\] |
\[\left( \mathbf{- \infty;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
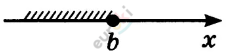| \[\mathbf{x < b}\] |
\[\left( \mathbf{- \infty;\ b} \right)\mathbf{-}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
Натуральные числа – это числа, которые используются ля подсчета чего-то конкретного (1, 2, 3, 4 и т.д.).
Круглая скобка означает, что точки a и b не входят во множество точек данного промежутка.
Квадратная скобка означает, что точки a и b входят во множество точек данного промежутка.
Решение.
\[\frac{a}{54} \in \left\lbrack \frac{1}{9};\frac{1}{6} \right\rbrack,\ \ a \in N\]
\[\frac{6}{54},\frac{7}{54},\frac{8}{54},\ \frac{9}{54}\ \in \left\lbrack \frac{1}{9};\frac{1}{6} \right\rbrack.\]
\[\boxed{\text{820.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[Пусть\ \text{x\ }\frac{км}{ч} - скорость\ \]
\[катера\ в\ стоячей\ воде,\ \]
\[тогда\ скорость\ катера\]
\[по\ течению\ (x + 2)\ \frac{км}{ч},\ \]
\[а\ (x - 2)\ \frac{км}{ч} - скорость\ \]
\[катера\ против\ \]
\[течения.\]
\[6 \cdot (x + 2) = 6x +\]
+\(12\ км - расстояние\ между\)
\[\ пристанью\ \text{M\ }и\ \]
\[пристанью\ \text{N.}\]
\[Составим\ уравнение:\]
\[\frac{6x + 12 - 40}{x + 2} +\]
\[+ \frac{6x + 12 - 40}{x - 2} = 9\]
\[\frac{6x - 28}{x + 2} + \frac{6x - 28}{x - 2} = 9\]
\[(6x - 28)(x - 2 + x + 2) =\]
\[= 9 \cdot \left( x^{2} - 4 \right)\]
\[12x^{2} - 56x = 9x^{2} - 36\]
\[3x^{2} - 56x + 36 = 0\]
\[D = 3136 - 432 = 2704\]
\[x_{1,2} = \frac{56 \pm \sqrt{2704}}{2 \cdot 3} = \frac{56 \pm 52}{6}\]
\[x_{1} = 18\ \left( \frac{км}{ч} \right) - скорость\ \]
\[катера.\ \]
\[x_{2} = \frac{4}{6} < 2\ \frac{км}{ч}\ \]
\[(не\ может\ быть).\]
\[Ответ:18\ \frac{км}{ч}.\]
