Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 813
Задание 813
\[\boxed{\text{813\ (813).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
| Обозначение и название числового промежутка. | Изображение числового промежутка на координатной прямой. |
|---|---|
|
\[\left\lbrack \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[числовой\ отрезок\ \] |
 |
|
\[\left( \mathbf{a;\ b} \right)\mathbf{- \ }\] \[\mathbf{интервал}\] |
 |
|
\[\left\lbrack \mathbf{a;\ b} \right)\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
|
\[\left( \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
|
\[\left\lbrack \mathbf{a; + \infty} \right)\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
|
\[\mathbf{(a; + \infty) -}\] \[\mathbf{открытый\ числовой\ луч}\] |
 |
|
\[\left( \mathbf{- \infty;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
|
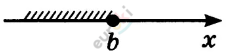\[\left( \mathbf{- \infty;\ b} \right)\mathbf{-}\] \[\mathbf{открытый\ числовой\ луч}\] |
 |
Решение.
\[\textbf{а)}\ отрезок\ \lbrack - 2;6\rbrack;\]
\[\textbf{б)}\ числовой\ луч\ \lbrack - 1;\ + \infty);\]
\[\textbf{в)}\ интервал\ ( - 1;7);\]
\[\textbf{г)}\ числовой\ луч\ ( - \infty;4\rbrack.\]
\[\boxed{\text{813.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[Пусть\ \text{x\ }\frac{км}{ч} - скорость\ \]
\[течения,\ скорость\ лодки\ \]
\[в\ стоячей\ воде\]
\[равна\ 90\ \frac{м}{мин} = 5,4\ \frac{км}{ч}\text{.\ }\]
\[\frac{6}{5,4 - x}\ ч - плыл\ рыболов\ \]
\[на\ веслах;\]
\[\frac{6}{x}\ ч - плыл\ без\ весел.\]
\[\frac{6}{5,4 - x} + \frac{6}{x} = 4,5\]
\[32,4 = 24,3x - 4,5x^{2}\]
\[4,5x^{2} - 24,3x + 32,4 =\]
\[= 0\ \ \ |\ :4,5\]
\[x² - 5,4x + 7,2 = 0\ \ \ | \cdot 10\]
\[10x² - 54x + 72 = 0\ \ \ |\ :2\]
\[5x^{2} - 27x + 36 = 0\]
\[D = 729 - 720 = 9\]
\[x_{1,2} = \frac{27 \pm \sqrt{9}}{2 \cdot 5} = \frac{27 \pm 3}{10}\]
\[x_{1} = 3\ \left( \frac{км}{ч} \right) - скорость\ \]
\[течения.\ \]
\[x_{2} = 2,4\ \left( \frac{км}{ч} \right) - скорость\]
\[\ течения.\]
\[Ответ:\ 3\ \frac{км}{ч}\ или\ \ 2,4\ \frac{км}{ч}.\]
