Решебник по алгебре 8 класс Макарычев ФГОС Задание 563

 

\[\boxed{\text{563\ (563).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }см - длина\ одного\ \]

\[катета,\ тогда\ (23 - x)\ см -\]

\[длина\ второго\ \]

\[катета.\ Известно,\ что\ площадь\ \]

\[треугольника\ равна\ 60\ см^{2}.\]

\[Формула:\ \ \ \]

\[S = \frac{\text{ab}}{2} \Longrightarrow 60 = \frac{\text{ab}}{2} \Longrightarrow ab = 120.\]

\[Составим\ уравнение:\]

\[x(23 - x) = 120\]

\[23x - x^{2} - 120 = 0\ \ \ \ \ \ | \cdot ( - 1)\]

\[x^{2} - 23x + 120 = 0\]

\[D = 529 - 4 \cdot 120 =\]

\[= 529 - 480 = 49\]

\[x_{1} = \frac{23 + 7}{2} = 15\ (см);\ \ \ \]

\[x_{2} = \frac{23 - 7}{2} = 8\ (см).\]

\[23 - x = 23 - 15 = 8\ (см).\]

\[23 - x = 23 - 8 = 15\ (см).\]

\[Ответ:8\ см\ и\ 15\ см.\ \]

\[\boxed{\text{563.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[S = 4\ 500\ см^{2}\]

\[a = 120\ см\]

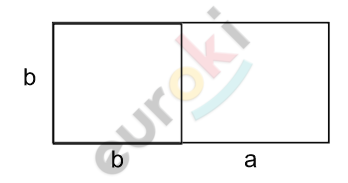
\[Пусть\ \text{b\ }см - ширина\ доски\ и\ \]

\[сторона\ квадрата.\]

\[(b + 120)\ см - первоначальная\]

\[\ длина\ доски.\]

\[S = a \cdot b = 4500\ см.\]

\[Составим\ уравнение:\]

\[(120 + b) \cdot b = 4\ 500\]

\[120b + b^{2} - 4500 = 0\]

\[b^{2} + 120b - 4500 = 0\]

\[D_{1} = (60)^{2} + 4500 =\]

\[= 3600 + 4500 = 8100\]

\[b_{1} = - 60 - 90 = - 150\ \]

\[(не\ подходит\ по\ условию).\]

\[b_{2} = - 60 + 90 = 30\ (см) -\]

\[сторона\ получившегося\ \]

\[квадрата.\]

\[Ответ:30\ см.\ \]