Решебник по алгебре 8 класс Макарычев ФГОС Задание 441

 

\[\boxed{\text{441\ (441).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ \frac{3x - 1}{2} + \frac{2 - x}{3} + 1 = 0\ \ \ \ \ \ | \cdot 6\]

\[3 \cdot (3x - 1) + 2 \cdot (2 - x) + 6 = 0\]

\[9x - 3 + 4 - 2x + 6 = 0\]

\[7x + 7 = 0\]

\[7x = - 7\]

\[x = - 7\ :7\]

\[x = - 1.\]

\[Ответ:x = - 1.\]

\[2 \cdot (y - 10) - 3 \cdot (5 - 2y) =\]

\[= 2,5 \cdot 12\]

\[2y - 20 - 15 + 6y = 30\]

\[8y = 65\]

\[y = 65\ :8\]

\[y = 8\frac{1}{8}.\]

\[Ответ:y = 8\frac{1}{8}.\]

\[\boxed{\text{441.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Представим выражение в виде квадрата суммы.

Выделим под корнем полный квадрат. Для этого рассмотрим слагаемое с корнем, которое будет представлять в формуле удвоенное произведение чисел a и b из формул:

\[a^{2} + 2ab + b^{2} = (a + b)^{2};\]

\[a^{2} - 2ab + b^{2} = (a - b)^{2}.\]

Рациональные числа (Q) – целые и дробные числа, которые можно записать в виде отношения m/n; m – целое число; n – натуральное число.

Иррациональные числа (I) – бесконечные десятичные непериодические дроби, которые нельзя представить в виде отношения m/n.

Решение.

\[\textbf{а)}\ \sqrt{13 + 4\sqrt{3}} - \sqrt{13 - 4\sqrt{3}} =\]

\[= \sqrt{\left( \sqrt{12} + 1 \right)^{2}} - \sqrt{\left( \sqrt{12} - 1 \right)^{2}} =\]

\[= \sqrt{12} + 1 - \sqrt{12} + 1 = 2 \in Q\]

\[\textbf{б)}\ \sqrt{19 - 2\sqrt{34}} + \sqrt{19 + 2\sqrt{34}} =\]

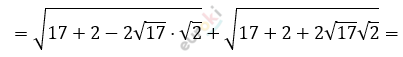
\[= \sqrt{\left( \sqrt{17} - \sqrt{2} \right)^{2}} + \sqrt{\left( \sqrt{17} + \sqrt{2} \right)^{2}} =\]

\[= \sqrt{17} - \sqrt{2} + \sqrt{17} + \sqrt{2} =\]

\[= 2\sqrt{17} \in I\]