Решебник по алгебре 8 класс Макарычев ФГОС Задание 440

 

\[\boxed{\text{440\ (440).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\mathbf{Воспользуемся\ формулами:}\]

\[\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{b}^{\mathbf{2}}\mathbf{=}\left( \mathbf{a - b} \right)\left( \mathbf{a + b} \right)\mathbf{;}\]

\[\mathbf{a}^{\mathbf{2}}\mathbf{+ 2}\mathbf{ab +}\mathbf{b}^{\mathbf{2}}\mathbf{=}\left( \mathbf{a + b} \right)^{\mathbf{2}}\mathbf{.}\]

Решение.

\[\frac{9 - x^{2}}{\mathbf{4}\mathbf{x}} \cdot \frac{\mathbf{8}\mathbf{x}}{x^{2} + 6x + 9} - 2 =\]

\[= \frac{(3 - x)(3 + x) \cdot 2}{(x + 3)^{2}} - 2 =\]

\[= \frac{2(3 - x) - 2(x + 3)}{x + 3} =\]

\[= \frac{6 - 2x - 2x - 6}{x + 3} = \frac{- 4x}{x + 3}\]

\[При\ x = - 2,5:\]

\[- \frac{4x}{x + 3} = - \frac{4 \cdot ( - 2,5)}{- 2,5 + 3} = \frac{10}{0,5} =\]

\[= \frac{100}{5} = 20.\]

\[\boxed{\text{440.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Воспользуемся формулами:

\[(a - b)^{2} = a^{2} - 2ab + b^{2};\]

\[(a + b)^{2} = a^{2} + 2ab + b^{2};\]

\[a^{2} - b^{2} = (a - b)(a + b).\]

Решение.

\[a² = \left( \sqrt{11 + \sqrt{85}} - \sqrt{11 - \sqrt{85}} \right)^{2} =\]

\[= 22 - 2\sqrt{11^{2} - \left( \sqrt{85} \right)^{2}} =\]

\[= 22 - 2\sqrt{121 - 85} =\]

\[= 22 - 2\sqrt{36} = 22 - 2 \cdot 6 =\]

\[= 22 - 12 = 10\]

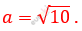
\[a^{2} = \left( \sqrt{3 + \sqrt{5}} + \sqrt{3 - \sqrt{5}} \right)^{2} =\]

\[= 6 + 2\sqrt{9 - 5} = 6 + 2\sqrt{4} =\]

\[= 6 + 2 \cdot 2 = 10\]