Решебник по алгебре 8 класс Макарычев ФГОС Задание 385

 

\[\boxed{\text{385\ (385).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ \sqrt{2} \cdot \sqrt{8} = \sqrt{2 \cdot 8} = \sqrt{16} = 4\]

\[\textbf{б)}\ \sqrt{27} \cdot \sqrt{3} = \sqrt{27 \cdot 3} = \sqrt{81} =\]

\[= 9\]

\[\textbf{в)}\ \sqrt{28} \cdot \sqrt{7} = \sqrt{28 \cdot 7} = \sqrt{196} =\]

\[= 14\]

\[\textbf{г)}\ \sqrt{2} \cdot \sqrt{32} = \sqrt{2 \cdot 32} = \sqrt{64} = 8\]

\[\textbf{д)}\ \sqrt{13} \cdot \sqrt{52} = \sqrt{13 \cdot 52} =\]

\[= \sqrt{13 \cdot 13 \cdot 4} = \sqrt{13^{2} \cdot 2^{2}} =\]

\[= 13 \cdot 2 = 26\]

\[\textbf{е)}\ \sqrt{63 \cdot 7} = \sqrt{63 \cdot 7} = \sqrt{441} =\]

\[= 21\]

\[\textbf{ж)}\ \sqrt{50} \cdot \sqrt{4,5} = \sqrt{50 \cdot 4,5} =\]

\[= \sqrt{225} = 15\]

\[\textbf{з)}\ \sqrt{1,2} \cdot \sqrt{3\frac{1}{3}} = \sqrt{\frac{12}{10} \cdot \frac{10}{3}} =\]

\[= \sqrt{\frac{12}{3}} = \sqrt{4} = 2\]

\[\boxed{\text{385.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Чтобы решить данные уравнения, сначала избавимся от знаменателя, умножив каждую дробь на число, равное НОК всех знаменателей.

Перенесем буквенную часть вправо, а числовую – влево, поменяв знаки слагаемых на противоположные.

Решение.

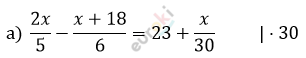
\[2x \cdot 6 - 5 \cdot (x + 18) =\]

\[= 23 \cdot 30 + x\]

\[12x - 5x - 90 = 690 + x\]

\[7x - x = 690 + 90\]

\[6x = 780\]

\[x = 130.\]

\[20 \cdot (x - 1) + 12 \cdot (2x + 1) =\]

\[= 15 \cdot (3x - 1)\]

\[20x - 20 + 24x + 12 =\]

\[= 45x - 15\]

\[44x - 45x = - 15 + 8\]

\[- x = - 7\]

\[\ x = 7.\]