Решебник по алгебре 8 класс Макарычев ФГОС Задание 260
Задание 260



\[\boxed{\text{260\ (260).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[y = \frac{k}{x}\]
\[\ y = kx + b\]

\[1 = \frac{k}{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[k = 2.\]

\[1 = 2 \cdot 2 + b\]
\[1 = 4 + b\]
\[b = - 3.\]
\[Ответ:при\ k = 2;\ b = - 3.\]

\[3 = \frac{k}{- 2}\]
\[k = - 6.\]

\[3 = ( - 6) \cdot ( - 2) + b\]
\[3 = 12 + b\]
\[b = - 9.\ \]
\[Ответ:при\ k = - 6;\ b = - 9.\]

\[1 = \frac{k}{- 1}\]
\[k = - 1.\]

\[1 = ( - 1)( - 1) + b\]
\[1 = 1 + b\]
\[b = 2.\ \]
\[Ответ:при\ k = - 1;\ b = 0.\]

\[\boxed{\text{260.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
Пояснение.
Область определения функции – это значения переменных, при которых выражение имеет смысл.
Точку, которая не входит в область определения, делаем «выколотой».
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби. Чтобы найти, при каких значениях x дробь не имеет смысла, нужно приравнять ее знаменатель к 0 и решить уравнение.
Произведение равно нулю, когда один из множителей равен нулю.
Формулы сокращенного умножения:
\[(a + b)^{2} = a^{2} + 2ab + b^{2};\]
\[(a - b)^{2} = a^{2} - 2ab + b^{2}.\]
Решение.
\[\textbf{а)}\ y = \frac{36}{(x + 1)^{2} - (x - 1)^{2}} =\]
\[= \frac{36}{4x} = \frac{9}{x};\ \ \ x \neq 0.\]
\[ООФ:(x + 1)^{2} - (x - 1)^{2} \neq 0\]
\[(x + 1)^{2} \neq (x - 1)^{2}\]
\[x^{2} + 2x + 1 \neq x^{2} - 2x + 1\]
\[4x \neq 0\]
\[x \neq 0.\]
| \[x\] | \[- 9\] | \[- 3\] | \[- 1\] | \[1\] | \[3\] | \[9\] |
|---|---|---|---|---|---|---|
| \[y\] | \[- 1\] | \[- 3\] | \[- 9\] | \[9\] | \[3\] | \[1\] |

\[\textbf{б)}\ y = \frac{18 - 12x}{x^{2} - 3x} - \frac{6}{3 - x} =\]

\[= \frac{6(3 - x)}{- x(3 - x)} = - \frac{6}{x}\]
\[ООФ:x^{2} - 3x \neq 0\]
\[x(x - 3) \neq 0\]
\[\ x \neq 0\]
\[x - 3 \neq 0\ \ \ \ \]
\[x \neq 3.\]
| \[x\] | \[- 6\] | \[- 3\] | \[- 1\] | \[1\] | \[3\] | \[6\] |
|---|---|---|---|---|---|---|
| \[y\] | \[1\] | \[2\] | \[6\] | \[- 6\] | \[-\] | \[- 1\] |

\[\textbf{в)}\ y = \frac{16}{(2 - x)^{2} - (2 + x)^{2}} =\]
\[= \frac{16}{(2 - x - 2 - x)(2 - x + 2 + x)} =\]
\[= \frac{16}{- 2x \cdot 4} = - \frac{2}{x}\]
\[ООФ:(2 - x)^{2} - (2 + x)^{2} \neq 0\]
\[(2 - x)^{2} \neq (2 + x)^{2}\]
\[4 - 2x + x^{2} \neq 4 + 2x + x^{2}\]
\[4x \neq 0\]
\[x \neq 0.\]
| \[x\] | \[- 4\] | \[- 2\] | \[- 1\] | \[1\] | \[2\] | \[4\] |
|---|---|---|---|---|---|---|
| \[y\] | \[0,5\] | \[1\] | \[2\] | \[- 2\] | \[- 1\] | \[- 0,5\] |
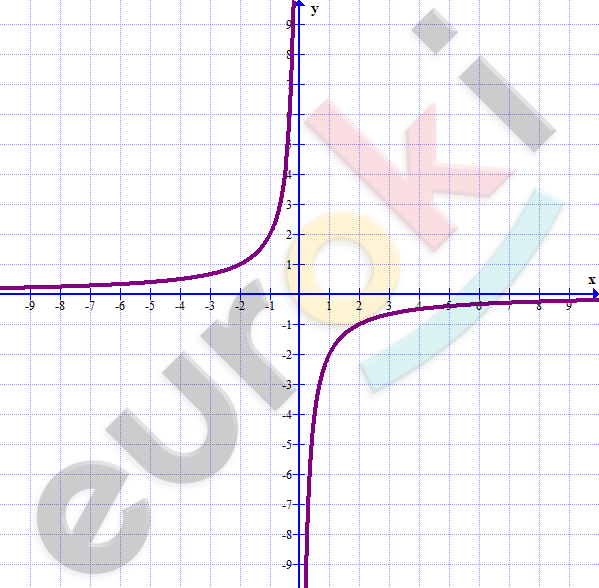
\[\textbf{г)}\ \ y = \frac{3x(x + 1) - 3x^{2} + 15}{x(x + 5)} =\]
\[= \frac{3x^{2} + 3x - 3x^{2} + 15}{x(x + 5)} =\]
\[= \frac{3(x + 5)}{x(x + 5)} = \frac{3}{x}\]
\[ООФ:\ \ x(x + 5) \neq 0\]
\[x \neq 0\ \ \]
\[x + 5 \neq 0\]
\[x \neq \ - 5.\]
| \[x\] | \[- 6\] | \[- 3\] | \[- 1\] | \[1\] | \[3\] | \[6\] |
|---|---|---|---|---|---|---|
| \[y\] | \[- 0,5\] | \[- 1\] | \[- 3\] | \[3\] | \[1\] | \[0,5\] |





