Решебник по алгебре 8 класс Макарычев ФГОС Задание 250

 

\[\boxed{\text{250\ (250).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ 1 - все\ салфетки\ \]

\[в\ одном\ заказе.\]

\[\frac{1}{8}\ (ч) - работала\ первая\ \]

\[вязальщица;\]

\[\frac{1}{9}\ ч - работала\ вторая\ \]

\[вязальщица;\]

\[\frac{1}{12}\ ч - работала\ третья\ \]

\[вязальщица.\]

\[1 + 1 + 1 = 3 - количество\ \]

\[объединенных\ заказов.\]

\[Найдем,\ через\ сколько\ часов\ \]

\[была\ закончена\ вся\ работа:\]

\[\frac{3}{\frac{1^{\backslash 9}}{8} + \frac{1^{\backslash 8}}{9} + \frac{1^{\backslash 6}}{12}} = \frac{3}{\frac{9 + 8 + 6}{72}} =\]

\[= \frac{3 \cdot 72}{23} = \frac{216}{23}\ часа = 9\frac{9}{23}\ часа.\]

\[Ответ:примерно\ \]

\[через\ 9\frac{9}{23}\ часа.\]

\[\boxed{\text{250.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[a^{3} + b^{3} + \left( \frac{b\left( 2a^{3} + b^{3} \right)}{a^{3} - b^{3}} \right)^{3} =\]

\[= \left( \frac{a\left( a^{3} + 2b^{3} \right)}{a^{3} - b^{3}} \right)^{3}\]

\[a^{3} + b^{3} =\]

\[= \left( \frac{a\left( a^{3} + 2b^{3} \right)}{a^{3} - b^{3}} \right)^{3} - \left( \frac{b\left( 2a^{3} + b^{3} \right)}{a^{3} - b^{3}} \right)^{3}\]

\[a^{3} + b^{3} =\]

\[= \frac{a^{3}\left( a^{3} + 2b^{3} \right)^{3}}{\left( a^{3} - b^{3} \right)^{3}} - \frac{b^{3}\left( 2a^{3} + b^{3} \right)^{3}}{\left( a^{3} - b^{3} \right)^{3}}\]

\[\left( a^{3} + b^{3} \right) \cdot \left( a^{3} - b^{3} \right)^{3} =\]

\[= a^{3}\left( a^{3} + 2b^{3} \right)^{3} - b^{3}\left( 2a^{3} + b^{3} \right)^{3}\]

\[\left( a^{3} + b^{3} \right)\left( a^{3} - b^{3} \right)\left( a^{3} - b^{3} \right)^{2} =\]

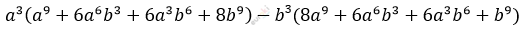
\[\left( a^{6} - b^{6} \right) \cdot \left( a^{6} - 2a^{3}b^{3} + b^{6} \right) =\]

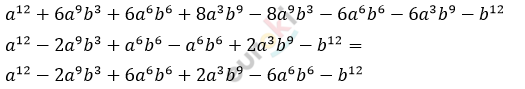
\[0 = 0 -\]

\[что\ и\ требовалось\ доказать.\]